Question

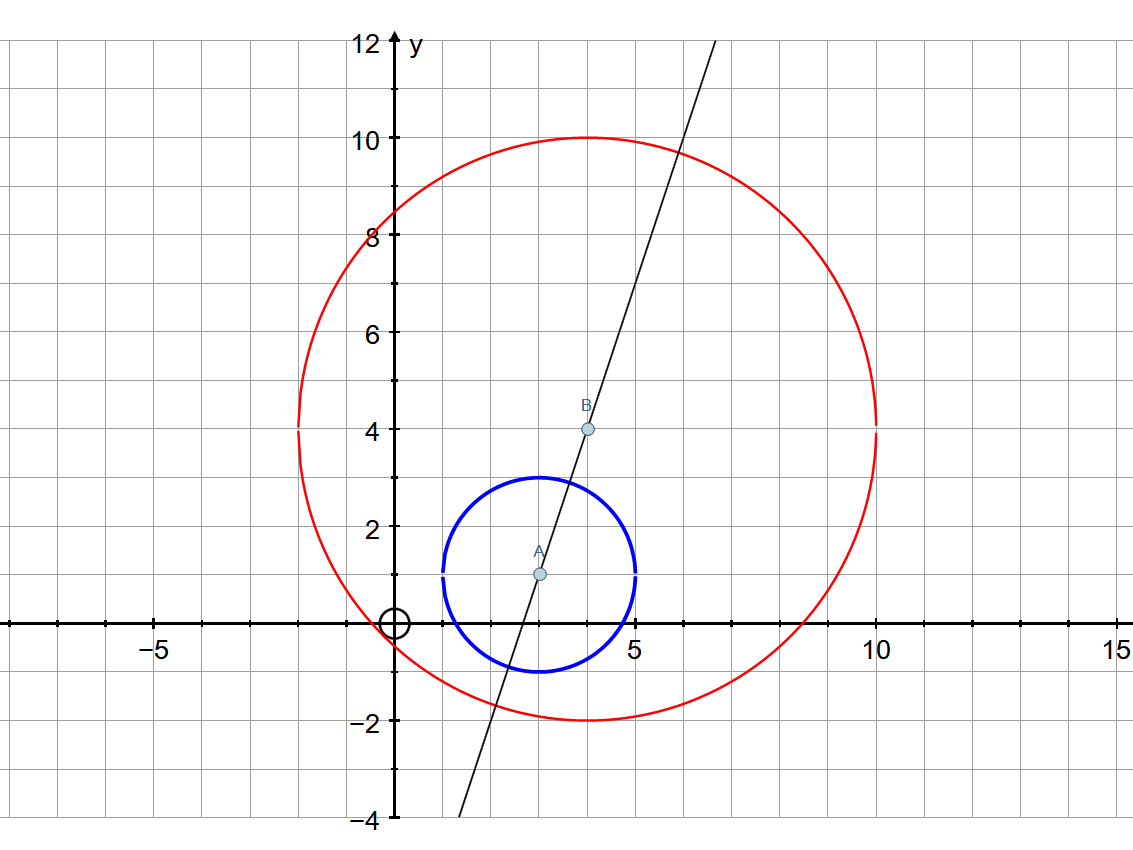
Circle A has a radius of `2` and a center of `(3 ,1 )`. Circle B has a radius of `6` and a center of `(8 ,5 )`. If circle B is translated by `<-4 ,-1 >`, does it overlap circle A? If not, what is the minimum distance between points on both circles?

Answer 1

See process below

Explanation:

Equation for `A`....`(x-3)^2+(y-1)^2=2^2`

Equation for `B`....`(x-8)^2+(y-5)^2=6^2`

A traslation is a isometric transformation, then the image for B in this movement is other circle of radius 6 and center in `(4,4)`. Thus we have the new equation for B is `(x-4)^2+(y-4)^2=6^2`

Obviously doesn`t overlap both circles and the minimum distance will lay in the line joining both centers

Lets calculate line equation

`(x-4)/1=(y-4)/3` or `3(x-4)=y-4` then `y=3x-8`
This line intercept to both circles in 4 points (see graph)

Distance is calculated by the standard formula (euclidean distance)

Lets see these points:
`A=(sqrt10/5+3,3sqrt10/5+1)`
`B=(-sqrt10/5+3,-3sqrt10/5+1)`
`C=(3sqrt10/5+4,9sqrt10/5+4)`
`D=(-3sqrt10/5+4,-9sqrt10/5+4)`

The minimum distance will be `BD=-sqrt10+4`

Answer 2

`color(blue)(4-sqrt(10)color(white)(888)"units"`

Explanation:

The general equation of a circle is:

`(x-h)^2+(y-k)^2=r^2`

Where:

`bbh` and `bbk` are the `x` and `y` coordinates of the centre respectively, and `bbr` is the radius.

Circle A

`(x-3)^2+(y-1)^2=4`

If B is translated by `((-4),(-1))`, then its centre is translated by this.

Centre:

`((8),(5))+((-4),(-1))=((4),(4))`

Circle B:

`(x-4)^2+(y-4)^2=36`

By using the distance between the centres and the radii we can deduce the following:

Let:

`d="distance between centres"`

`r_1,r_2="radii"`

If:

`d > r_1+r_2` Then the circles do not touch.

`d < r_1+r_2` Then the circles intersect at two points or one circle is contained in the other.

`d=r_1+r_2` Then the circles touch at one point.

Using the distance formula:

`d=sqrt((3-4)^2+(1-4)^2)=sqrt(10)`

Sum of radii:

`2+6=8`

`sqrt(10)<8`

So the circles intersect at two points or one is contained in the other. This can be tested by noticing that if the diameter of the smaller circle is less than the radius of the larger then the smaller circle is contained in the larger one.

Diameter of smaller circle is `4`

Radius of larger circle is `6`

So smaller circle is contained in the larger.

To find the shortest distance:

`"radius of B"-("radius of " A+d)`

`6-(2+sqrt(10))=4-sqrt(10)color(white)(888)"units"`

PLOT: