A circle's center is at #(9 ,1 )# and it passes through #(5 ,4 )#. What is the length of an arc covering #(pi ) /3 # radians on the circle?
2 Answers
Equation circle centered in a generic point is
In our case
Circle pases by
So the radius is
Now: we know that a circle has a lenght of
If
The length of the arc is :
Explanation:
We have a circle with center
Let ,
Let ,
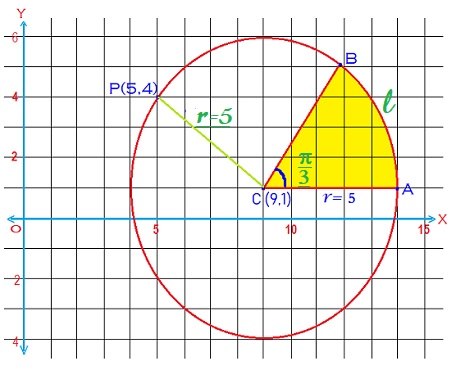
We know that the radius of circle is
#r=CP#
So, the length of the arc is :

