Question

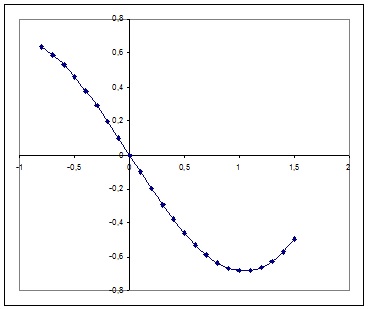
How do I find the maximum and minimum values of the function `f(x) = x - 2 sin (x)` on the interval `[-pi/4, pi/2]`?

Answer 1

You can derive your function and set your derivative equal to zero. The value(s) of `x` you'll find will be the points of maxima or minima.

In your case you have:

`f'(x)=1-2cos(x)`

Setting `f'(x)=0` gives:

`1-2cos(x)=0`
When `x=pi/3`

You can now analyze when the derivative is bigger than zero:

`1-2cos(x)>0`
i.e. when `x>pi/3`

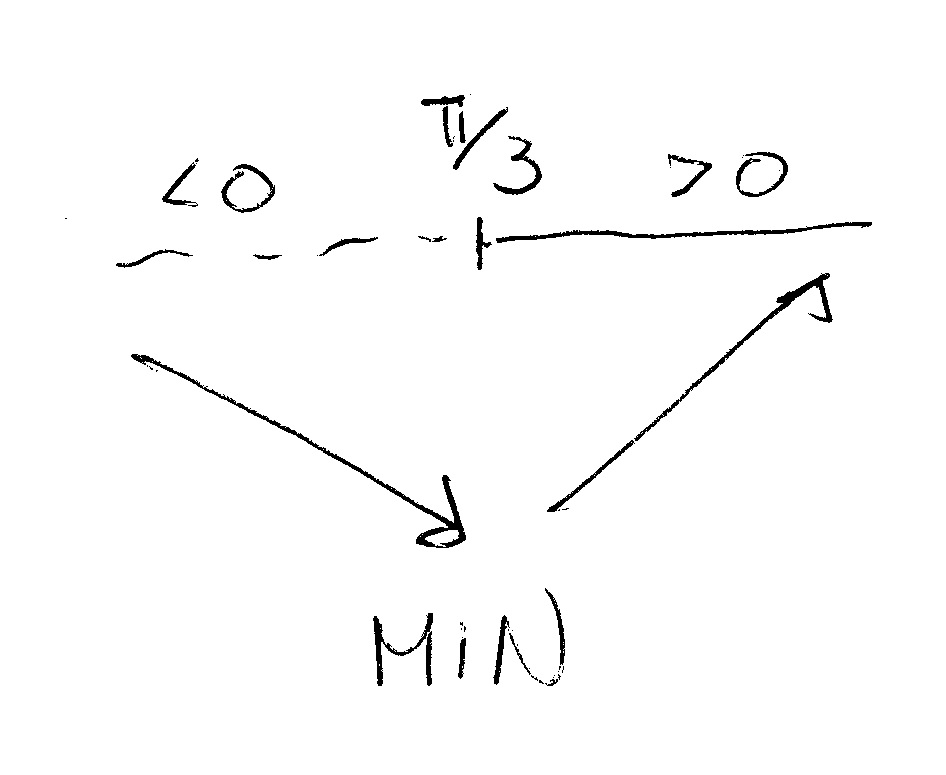
Your value of `x=pi/3` represent a minimum for your function, and in your interval you get the graph: