Let's look at what the graphs of #sin(x)# and #x/n# might look like for a sample #n#, say #n=10#:
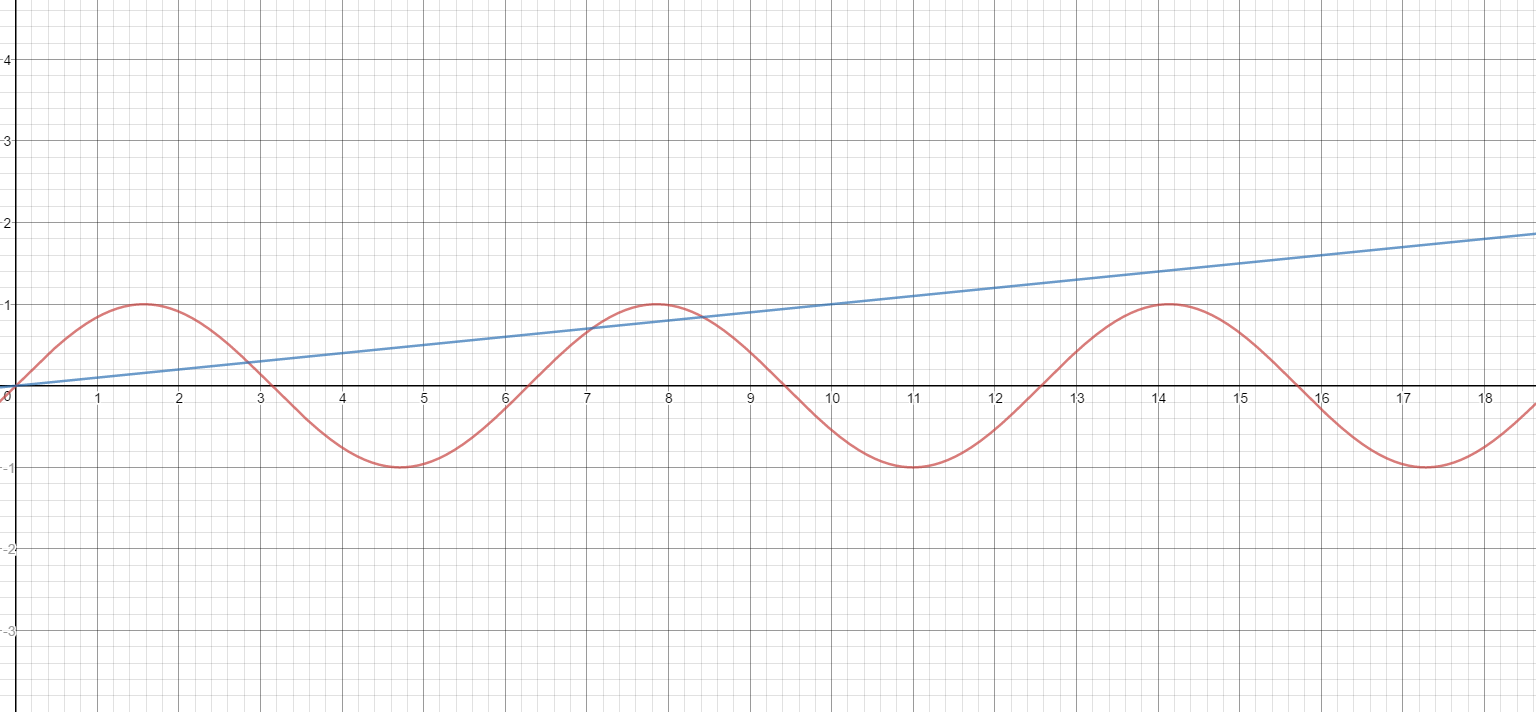
Notice that as long as #x/n<1#, two solutions (intersections) are generated on each interval #[2kpi, (2k+1)pi], k in ZZ^+#, that is, on each positive "hump" for #sin(x)#. As we are only looking for positive solutions, we can disregard #x=0#, meaning the first hump only gives a single solution.
With the above observations, we can tell that if the line #x/n# passes through #k# humps, then we generate #2k-1# positive solutions. As we are looking for #69# positive solutions, solving for #k# shows that we need #x/n# to pass through #35# humps.
Before continuing, note that #sin(x)=1# has no integral solutions, meaning #sin(x)=1# implies #x/n!=1#. This allows us to know that the line #x/n# either passes under #sin(x)# at the peak of a hump, thus generating two solutions, or passes over it, generating none.
If we look at the intervals on which #sin(x)# is positive, we find them to be of the form #[0, pi], [2pi, 3pi], [4pi, 5pi], ...#. The #35^"th"# interval will thus be #[68pi, 69pi]#. To get exactly #69# solutions, then, we must have #x/n < 1# at the midpoint of #[68pi, 69pi]# and #x/n > 1# at the midpoint of #[70pi, 71pi]#.
Put in terms of inequalities, this gives us
#((137pi)/2)/n < 1 < ((141pi)/2)/n#
#=> (137pi)/2 < n < (141pi)/2#
As #(137pi)/2 ~~ 215.2# and #(141pi)/2 ~~221.5#, we get our solution set as
#n in {216, 217, 218, 219, 220, 221}#


