Question

How do you use the disk or shell method to find the volume of the solid generated by revolving the region bounded by the graphs `y=(18/x^2)`, `y=0`, `x=1`, `x=9` about the line `y = 18`?

Answer 1

`V = 12640/27pi ~~ 4620 " unit"^3`

Explanation:

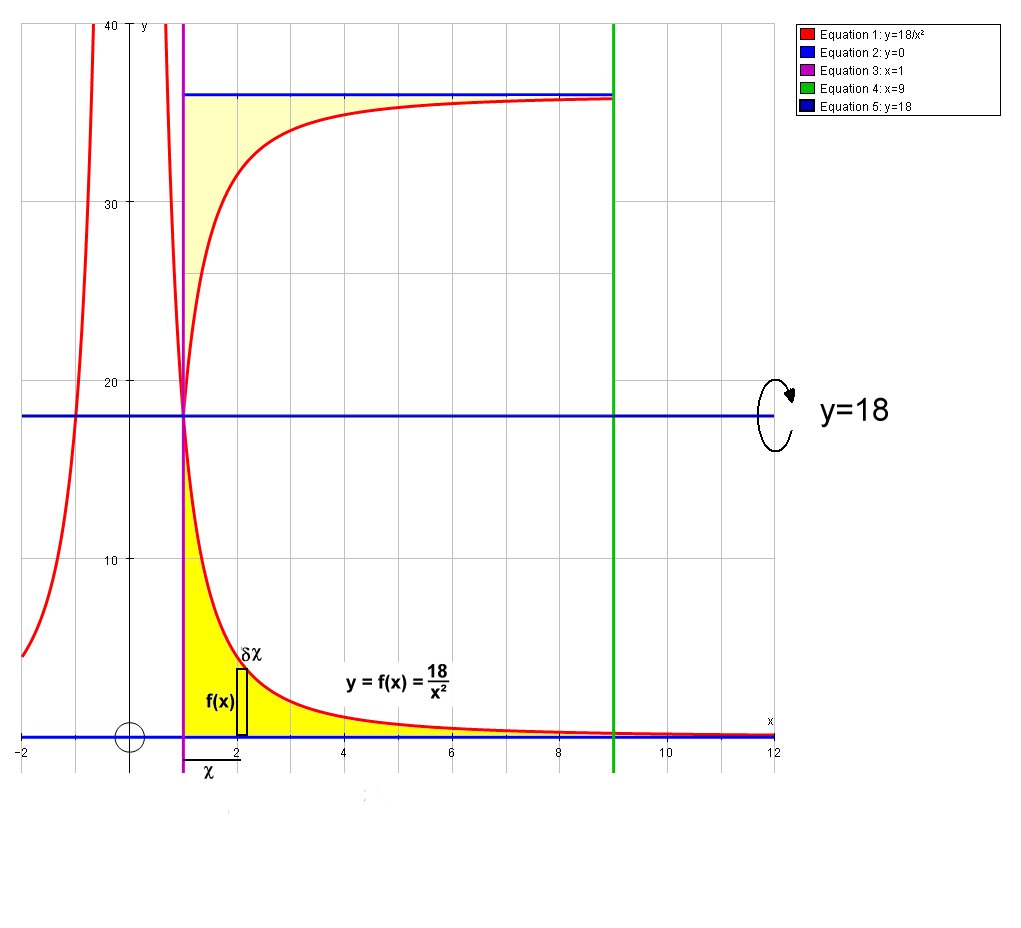
The darker yellow shaded area is the region of rotation, which is bounded by `y=18/x^2`, `x=1`, `x=9` and `y=0`, and we want to rotate about the line `y=18`.

Imagine an almost infinitesimally thin vertical line of thickness
`delta x` between the `x`-axis and the curve at some particular
`x`-coordinate. If this is rotated about the line `y=18` it would formal a "washer" with the following properties;

`{: ("Outer radius",=18), ("Inner radius",=18-f(x)), ("Thickness ",= delta x) :}`

And so the volume of this "washer" would be given by

`\ \ \ \ \ delta V~~ pi("outer")^2delta x - pi("inner")^2delta x`
`:. delta V~~ pi{ ("outer")^2 - ("inner")^2 } delta x`

If we add up all these infinitesimally thin cylinders over the appropriate `x` range then we would get the precise total volume `V` given by:

`V=int_(x=a)^(x=b) pi{ ("outer") - ("inner")^2 } dx`

So for this problem we have:

`\ \ \ \ \ V=int_1^9 pi( 18^2 - (18-18/x^2)^2) dx`
`:. V = pi int_1^9 ( 18^2 - (18^2-2*18*(18/x^2)+(18/x^2)^2) dx`
`:. V = pi int_1^9 ( 324 - (324-648/x^2+324/x^4)) dx`
`:. V = pi int_1^9 ( 648/x^2-324/x^4) dx`
`:. V = 324pi int_1^9 ( 2/x^2-1/x^4) dx`
`:. V = 324pi int_1^9 ( 2x^-2-x^-4) dx`
`:. V = 324pi [-2x^-1+x^-3/3]_1^9`
`:. V = 324pi [-2/x+1/(3x^3)]_1^9`
`:. V = 324pi {(-2/9+1/(3*9^3)) - (-2/1+1/3) }`
`:. V = 324pi {(-2/9+1/2187) - (-2+1/3) }`
`:. V = 324pi {(-415/2187) - (-5/3) }`
`:. V = 324pi *3160/2187`
`:. V = 12640/27pi`
`:. V ~~ 4620 " unit"^3`