Question

Question #adbb5

Answer 1

Trapezium Rule gives:

`int_1^4(4-x^2) \ dx ~~ -9.1250` (to 4dp)

Simpson's Rule gives:

`int_1^4(4-x^2) \ dx ~~ -9.0000` (to 4dp)

Exact Answer:

`int_1^4(4-x^2) \ dx = -9`

Explanation:

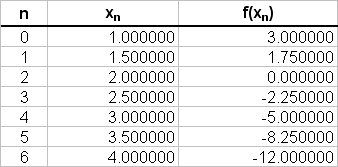
The values of `f(x)=4-x^2` are tabulated as follows (using Excel) working to 6dp. Step size is unspecified so I will use `n=6` in both cases.

Trapezium Rule

`int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}`

The trapezium rule uses a series of two consecutive ordinates and a best fit straight line to form trapeziums to approximate the area under a curve, It will have 100% accuracy if `y=f(x)` is a straight line and typically provides a good estimate provided `n` is chosen appropriately.

So,

`int_1^4(4-x^2) \ dx = 0.5/2 { 3 -12 + 2(1.75 + 0 -2.25 -5 -8.25)}`
`" " = 0.25 { -9 + 2( -13.75 )}`
`" " = 0.25 { -9 -27.5 }`
`" " = 0.25 { -36.5 }`
`" " = -9.125`

Simpson's Rule:

`int_a^b f(x) \ dx ~~ h/3{(y_0+y_n)+4(y_1+y_3+...)+2(y_2+y_4+...)}`

Simpson's rule uses a series of three consecutive ordinates and a best fit parabola to approximate the area under a curve, It will have 100% accuracy if `y=f(x)` is a parabola, and generally provides a better approximation than the Trapezium rule

So:

`int_1^4(4-x^2) \ dx = 0.5/3 { (3 -12) + 4(1.75 -2.25 -8.25) + 2(0 -5) }`
`" " = 0.166666 {-9 + 4(-8.75) + 2(-5) }`
`" " = 0.166666 {-9 -35 -10 }`
`" " = 0.166666 {-54 }`
`" " = -9`

Exact Value:

`int_1^4(4-x^2) \ dx = [4x-1/3x^3]_1^4`
`" " = {16-64/3}-{4-1/3}`
`" " = -16/3-11/3`
`" " =-9`