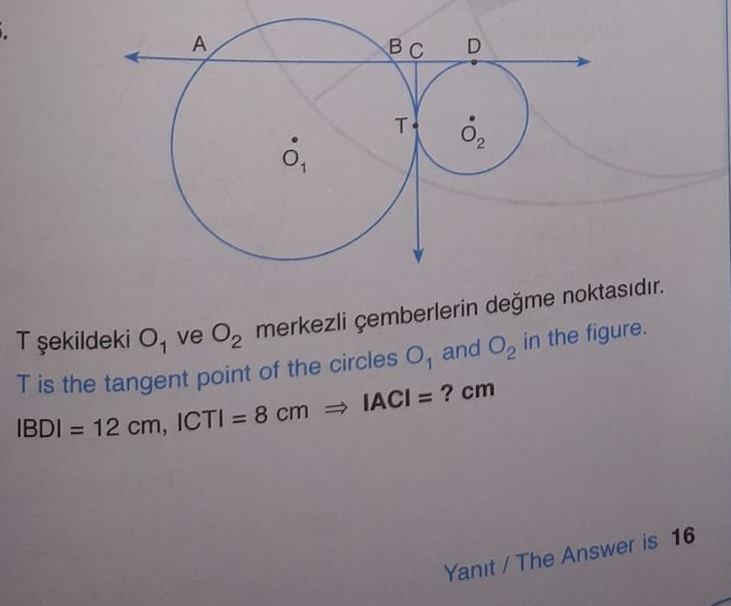
How length of /AC/ = ?
1 Answer
Nov 2, 2017
Explanation:
As two tangent segments to a circle from an external point are equal in length,
As
Proof of tangent-secant theorem is available in the link below:
https://socratic.org/questions/let-m-be-a-point-and-c-a-circle-m-doesn-t-belong-to-the-c-let-a-and-b-be-points-#471096
