Question

How do you Solve 6sin(x)+5cos(x)=4? What are the first 2 positive solutions?

Answer 1

See below.

Explanation:

`6sinx+5cosx=4`

Subtract `5cosx` from both sides:

`6sinx=4-5cosx`

Square both sides:

`36sin^2x=(4-5cosx)^2`

`36sin^2x-(4-5cosx)^2=0`

Identity:

`color(red)bb(sin^2x=1-cos^2x)`

`36(1-cos^2x)-(4-5cosx)^2=0`

Expand and simplify:

`36-36cos^2x-(16-40cosx+25cos^2x)=0`

`36-36cos^2x-16+40cosx-25cos^2x=0`

`20-61cos^2x+40cosx=0`

`61cos^2x-40cosx-20=0`

Let : `u=cosx`

`61u^2-40u-20=0`

Using the quadratic formula:

`u=(-(-40)+-sqrt((-40)^2-(4(61)(-20))))/(2(61))`

`u=(40+-sqrt(1600-(-4880)))/122`

`u=(40+-sqrt(6480))/122=(20+-18sqrt(5))/61`

`u = cosx`

`cosx=(20+-18sqrt(5))/61`

`=arccos(cosx)=arccos((20+18sqrt(5))/61)=>x`

`=arccos((20+18sqrt(5))/61)+2pik~~0.15706+pik`

`2pi-arccos((20+18sqrt(5))/61)+2pik~~6.12613+2pik`

`=arccos(cosx)=arccos((20-18sqrt(5))/61)=>x`

`=arccos((20-18sqrt(5))/61)+2pik~~1.90917+pik`

`=-arccos((20-18sqrt(5))/61)+2pik~~4.37401+pik`

If we test these solutions we find only:

`arccos((20-18sqrt(5))/61)+2pik~~1.90917+pik`

`2pi-arccos((20+18sqrt(5))/61)+2pik~~6.12613+2pik`

Are true.

The first two positive values are:

`arccos((20-18sqrt(5))/61)+2pik~~1.90917+pik` with `k=0`

`2pi-arccos((20+18sqrt(5))/61)+2pik~~6.12613+2pik` with `k=0`

`k in ZZ`

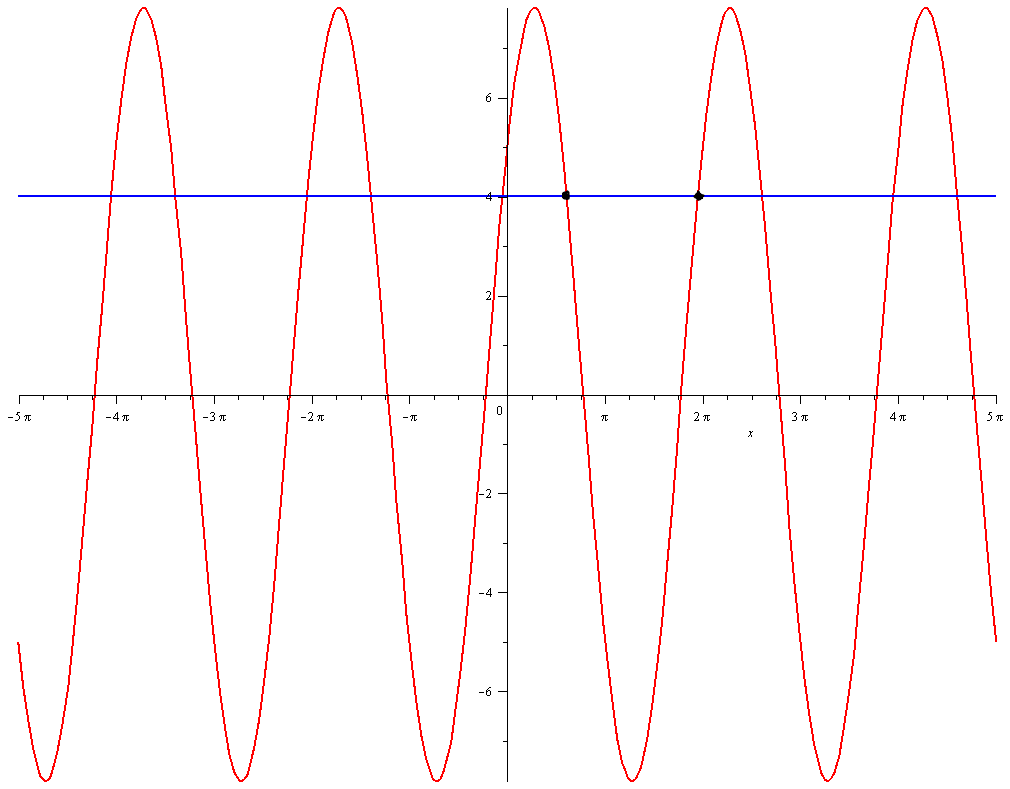
The graph verifies this: