How do you FOIL #(4z-u)(3z+2u)#?
3 Answers
The FOIL'ed version of the factored expression is
Explanation:
As you may know, FOIL stands for First Outer Inner Last. Using this Mnemonic, we'll work in order.
First:
Outer:
Inner:
Last:
Now, let's put them back together in the expression:
Finally we combine like terms to get our finished expression:
Explanation:
The FOIL method:
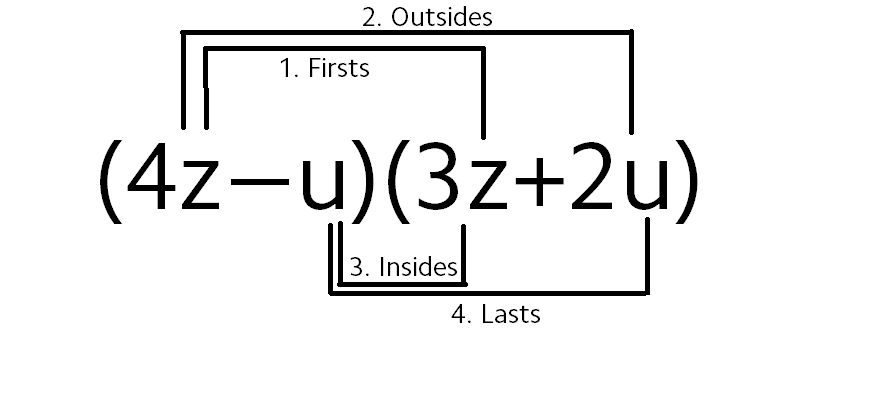
#(4z−u)(3z+2u)# #(4z*3z) +(4z * 2u) + (-u*3z) + (-u * 2u)# #12z^2 +8zu -3zu - 2u^2# #12z^2 +5zu -2u^2#
Hope this helps!
Explanation:
Since
and get
The inside would be
In which
Finally, you solve the last two...
Which equals
You're equation should now look like this;
Subtract
You should get
Your final equation should look like this;



