Question

2 identical pendulums A&B are suspended from same point.The bobs A&B are given positive charges q1 and q2 (q1<q2). If A&B are making angles $1 and $2 with the vertical and T1 and T2 are tensions in the string respectively.Then prove that $1=$2 and T1=T2?

Answer 1

This is usually considered to be "obvious" from the symmetry of the problem. It turns out that proving this directly is not entirely trivial - see below.

Explanation:

From the diagram :

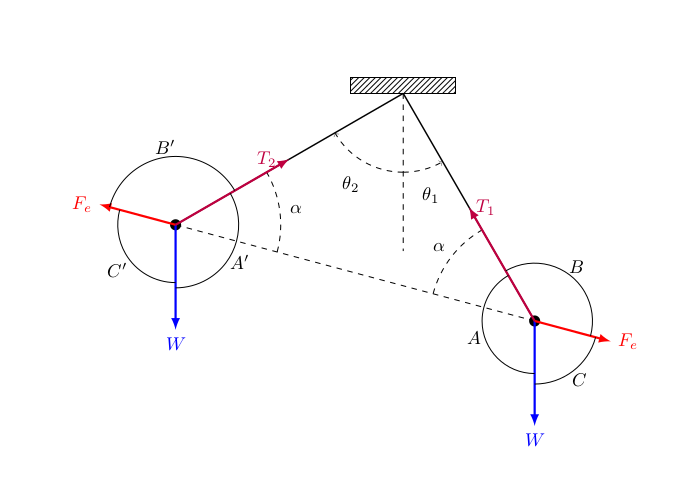
it is obvious (since the two pendulums are identical) that

`alpha = 1/2(pi-theta_1-theta_2) = pi/2-(theta_1+theta_2)/2`

It is also quite easy to work out that

`A = pi-theta_1,qquad A^'=pi-theta_2`

`B = pi-alpha = pi/2+(theta_1+theta_2)/2 = B^'`

and

`C = 2pi-(A+B) = pi/2-(theta_2-theta_1)/2,`
`C^' = pi/2+(theta_2-theta_1)/2`

We can arrive at the final proof most readily by means of Lamé's theorem (https://en.wikipedia.org/wiki/Lami%27s_theorem), which states that

When three forces are in equilibrium, their magnitudes are proportional to the sine of the angle between the other two.

(This is a simple consequence of the sine law for triangles)

Thus

`F_e/sinA = W/sin B = T_1/sin C`

`F_e/(sinA^') = W/(sin B^') = T_1/sin C^'`

Note that the two masses are identical, and the magnitudes of Coulomb repulsion acting on the two charges are the same.

These ratios can be rewritten as

`F_e/(sintheta_1) = W/cos((theta_1+theta_2)/2) = T_1/cos((theta_2-theta_1)/2)`

and

`F_e/(sintheta_2) = W/cos((theta_1+theta_2)/2) = T_2/cos((theta_2-theta_1)/2)`

So, obviously

`T_2/W = cos((theta_2-theta_1)/2)/cos((theta_1+theta_2)/2)=T_1/W implies T_1=T_2`

`F_e/W = sin theta_1/cos((theta_1+theta_2)/2)=sin theta_2/cos((theta_1+theta_2)/2) implies theta_1=theta_2`

Answer 2

Another way of proving this result is by using energy considerations. I will use the same diagram and conventions used in my previous answer https://socratic.org/s/aQbwm9py

Explanation:

In equilibrium, the total potential energy of the system will be the least possible. Note that this consists of the electrostatic potential energy of the charges and the gravitational potential energy - tension, being a no-work force, does not contribute. Of these, the first term depends on the distance between the two charges - and this in turn depends only on the angle `theta_1+theta_2` between the two strings. So, if the angles change while maintaining a fixed sum, the electrostatic potential energy will stay unchanged.

This means that in equilibrium, the angles `theta_1` and `theta_2` will take a value such that the gravitational potential energy

`-mgl(costheta_1+costheta_2)`

(here we have taken the gravitational potential energy )will be the least subject to a constant value of `theta_1+theta_2`.

This implies that in equilibrium `costheta_1+costheta_2` must be maximum (of course subject to `theta_1+theta_2=` constant). Now

`costheta_1+costheta_2 = 2cos((theta_1+theta_2)/2)cos((theta_1-theta_2)/2)`

so for this to be maximum at a fixed value of `theta_1+theta_2`, `cos((theta_1-theta_2)/2)` must be the largest possible. Thus,

`theta_1-theta_2 = 0qquad implies qquad theta_1=theta_2`

Note
Minimizing the total potential energy (electrostatic+gravitational) with respect to the common value `theta` can be a simple way of finding the angle that each string makes with the vertical.