Question

Question #1f344

Answer 1

I tried this hoping I didn't confuse you even more!

Explanation:

These things you are using here are sines and cosines of angles....BUT...you can have a lot of angles!!!
The difficult thing is that if you have `sin(30^2)` it gives you a value that is the same as if you use the angle `360^@+30^@=390^@`!!!!
In fact:
`sin(30^@)=0.5`
and
`sin(390^@)=0.5`

Sometimes to avoid to have these possibilities they reduce the interval so that you cannot go further than `360^@` or `180^@`.
Here it seems difficult because they use radians where `180^@=pi` but it is the same idea. They need a result for angles between `0^@` and `pi=180^@` no more than that....
Ok...
To solve your equation you have to operate as in a normal equation BUT the only problem is that the unknown is an angle inside a sine or cosine.
Let us try your case:
`2sin(x/2)=sin(x)`
we need to change the argument of the first sin into `x` to be able to combine with the other and have all with only `x` as argument. We use a Trigonometric Identity:

You can find them on the internet or at:
http://www.onlinemathlearning.com/trig-identities.html

at the bottom right we see that: `sin(x/2)=+-sqrt((1-cos(x))/2)`
let us substitute:

`2[color(red)(+-sqrt((1-cos(x))/2))]=sin(x)`
square both sides:

`cancel(4)^2(+-(1-cos(x))/cancel(2))=sin^2(x)`

use the Pythagorean identity (top right) and write:

`2(1-cos(x))=1-cos^2(x)`

rewrite it as:

`cos^2(x)-2cos(x)+1=0`

which is a second degree equation!!!!
Instead of `x^2` you have `cos^2(x)` but it is the same....we use the Quadratic Formula:

`cos(x)=(2+-sqrt(4-4))/2=1`

now the tricky part...when is it that `cos(x)=1` or for which angle `x`????
Let us see at the graph of `cos(x)` BUT only in the interval `[0,pi]` (grey square):

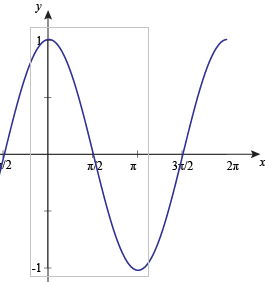
You can see that `cos(x)=1` only when the angle is...`x=0`!!!!