What is #cosx#?
2 Answers
See explanation...
Explanation:
This question can be answered in many different ways at different levels of rigour and knowledge.
Here are a few ideas:
-
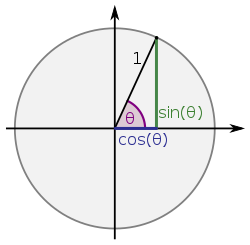
Starting from the point
#(1, 0)# , travel a distance#x# anticlockwise around the unit circle. The#x# coordinate of the point you reach will be#cos(x)# .
-
The function
#cos(x)# is defined by the series:
#cos(x) = 1/(0!)-x^2/(2!)+x^4/(4!)-x^6/(6!)+... = sum_(n=0)^oo (-1)^nx^(2n)/((2n)!)#
- The function
#cos(x)# is the real part of the function#e^(ix)# where:
#e^t = 1/(0!)+t/(1!)+t^2/(2!)+t^3/(3!)+... = sum_(n=0)^oo t^n/(n!) = lim_(n->oo) (1+t/n)^n#
- The function
#cos(x)# is the unique analytic function satisfying:#{ (cos(0) = 1), (cos^((1))(0) = 0), (cos^((2))(x) = -cos(x)) :}#
#color(white)()#
where#cos^((1))(x)# and#cos^((2))(x)# denote the first and second second derivatives of#cos(x)# .
(The second condition is required to exclude functions of the form#cos(x)+k sin(x)# with#k != 0# ).
See below.
Explanation:
To avoid confusion between the variable name and the usual names of the axes on the 2D plane, I will define
Imagine a circle of radius 1 on the
A point
Then, by definition,
Similarly,
We can better understand these functions' relation to the unit circle as follows:
Remember,
Now, consider the right angled triangle formed by the points,
Then:
From basic Trig definitions:
NB: By applying Pythagoras' theorem to

