Question

Question #bf476

Answer 1

See below.

Explanation:

I'm not really sure what you mean by "rather mathematically". By the look of it, you are trying to show it in terms of the sides of a right angled triangle.

`tanx=o/a`

`sin(x)=o/h`

`cos(x)=a/h`

`:.`

`o/a=(o/h)/(a/h)`

RHS:

Multiply by `h`

`((ho)/h)/a`

Divide by `a`

`(ho)/(ha)`

Cancel:

`o/a`

Answer 2

Yes, there is a way. You're on the right tracks, but there's also another way which takes us back to where the trigonometric functions come from.

Explanation:

We can prove this the way you are doing this.

`sinx=(O)/H`
`cosx=A/H`

`sinx/cosx= (O)/(H)-:A/H`
`=(O)/cancelHxxcancelH/A`
`=(O)/(A)=tanx` as required.

The other way to prove this is to go back to where the trigonometric functions come from in the first place.

Take a unit circle. This is a circle, radius 1.

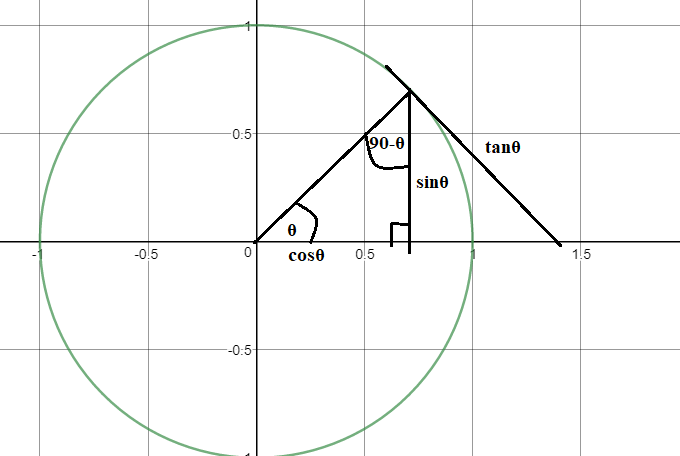
(all angles are measured in degrees from this point on).

Let us make a right-angled triangle from the origin, with the hypotenuse being the radius. This triangle has an angle `theta` (theta) to the x-axis.

We will give this triangle a height of `sintheta`. This is the side opposite to the angle. Since the hypotenuse is 1 (as is the radius), `O=sintheta`

This triangle has another non-right-angle, however. This angle is `90-theta`. This angle is known as complementary to `theta`, which means that they sum to `90^o`.

The line adjacent to our original angle `theta` is the line opposite to our complementary angle `90-theta`. So `A=sin(90-theta)`. Since this the sin of the complementary angle, we shall call this the complementary sine, cosine. `A=costheta`

The other thing we can do is to draw a tangent to the unit circle from the "top" of the triangle to the x-axis. We will call this length `tantheta`.

Since a tangent meets a radius at a right angle, this gives us two triangles.

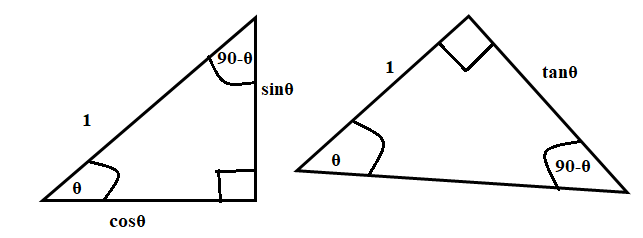
The first triangle on the left is our triangle with a radius 1 from the unit circle, and sides `sintheta` and `costheta` from above. The triangle on the right has a base of the x-axis, a side of 1 from the unit circle and the other of `tantheta` from our tangent. It has a right angle from where a tangent meets a radius.

Since both of these triangles all have the same angles (`90-theta-(90-theta)`, they are mathematically similar.

We can find the scale factors of these triangles. By looking at the length between the angle `theta` and the right angle, there is a scale factor of `1/costheta`. The scale factor by looking at the sides between `90-theta` and the right angle is `tantheta/sintheta`

Since this is the same scale factor in both cases:

`1/costheta=tantheta/sintheta`

By multiplying both sides by `sintheta`

`sintheta/costheta=tantheta` as required.