Question

What is `sin` ?

Answer 1

A few thoughts...

Explanation:

`sin theta` (sine), `cos theta` (cosine) and `tan theta` (tangent) are trigonometric functions.

One way of understanding them is as the ratios of the sides of right angled triangles.

For example, here's a right angled triangle with sides `3`, `4` and `5`...

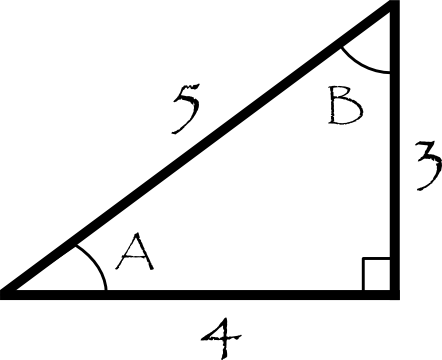
Applying `sin`, `cos` and `tan` to the angle `A`, we have:

`sin A = "opposite"/"hypotenuse" = 3/5`

`cos A = "adjacent"/"hypotenuse" = 4/5`

`tan A = "opposite"/"adjacent" = 3/4`

Due to Pythagoras' theorem, we find that:

`(sin A)^2 + (cos A)^2 = 1`

for any angle `A`.

Note that you will often see `(sin theta)^2` written as `sin^2 theta`. This is a common shorthand.

There is much more that could be said, but if you have only just come across `sin` for the first time, then that may be enough for now.

Answer 2

Please see below.

Explanation:

Sin is the abbreviated name for something called the sine. It is a topic of study in trigonometry. (tri - three, gon -- angle, metron -- measure)

There are several ways of "getting at" the sine, but probably the best approach to start with involves geometry.

In geometry, two figures are called "similar" if we can label sides so that corresponding sides are proportional.

(Get something to write with and something to write on.)
A triangle with sides of length `3`, `4` and `5` is similar to a triangle with sides of length `8`, `10` and `6`. But not in that order. To make them correspond we need to write:

sides of length `3`, `4` and `5` correspond to

sides of length `6`, `8` and `10`.

Now take the ratio of any two sides in the first triangle. It will be equal (proportional) to the corresponding two sides of the other triangle.

Here is a picture of a right triangle. The legs (the short sides) are labeled compared to the angle at `A`. The side `a` is "Opposite" the angle at `A`. The side `b` is "Adjacent" to the angle at `A`. and the "Hypotenuse" is the third side (the longets and the side opposite the `90^@` angle.

Now, any right triangle that has angle `A` congruent (equal measure) to this one is a similar triangle. So the ratio of the corresponding sides on any right triangle with an angle equal to `A` will be the same as the ratio of the sides in this particular triangle.

With `3` sides, we can form `6` ratios: `a/b`, `a/c`, `b/c` and the reciprocals `b/a`, `c/a` and `c/b`.

We have names for each of these ratios that refer back to the angle `A`.

The sine of `A`, written `sinA` is the ratio: `a/c`.

Using geometry we can prove that if the angle at `A` measures `30^@` and side `a` measures `5`, then side `c` must measure `10`. (That is just an example.)

And once we have done that we can be sure that in any right triangle with a `30^@` angle in it, the ratio of the side opposite the `30^@` angle to the hypotenuse is equal to `5/10` or `1/2`

We say that the sine of `A`, written `sinA` is the ratio: `1/2`.