This has got to be one of my favourite problems in mathematics...
Let #H# be the probability of flipping heads
Let #T# be the probability of flipping tails
#H and T# is not nessesarily #= 1/2# as its unfair...
Now we must use our knowledge of expected outcomes...
#E(X) = sum x_i P(X=x_i) = sumx_i p_i #
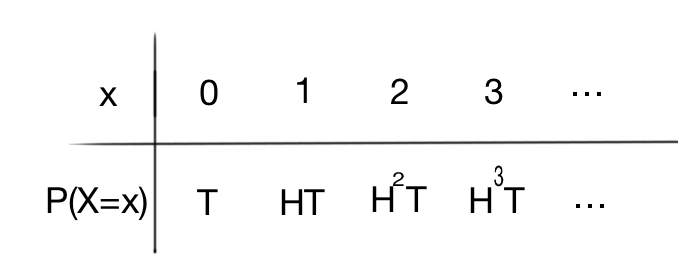
Now we can devise a descrete random variable #X#:
#X# - Number of wins...
Getting 0 wins would have a probability of #T#
Getting 1 win is getting a head and then tails, #HT#
.
.
.
Hence we must use our #E(X) # formula...
#E(X) = (0*T) + (1*HT) + (2*H^2T) + (3*H^3T) + ...#
#=> E(X) = HT + 2H^2 T + 3H^3 T + ... #
Now factoring out #HT#:
# => E(X)= HT ( 1 + 2H + 3H^2 + 4H^3 + ... )#
This stage is the most difficult, we must recognise that:
# 1 + 2H + 3H^2 + ... = d/(dH) ( H + H^2 + H^3 + ... ) #
#=> E(X) = HT * d/(dH) ( H + H^2 + H^3 + ... ) #
Now we know #H + H^2 + H^3 + ... # is a infinte geometric series...
We know: #sum_(n=1) ^oo a*r^(n-1) = a/(1-r) ,|r|<1 #
#=> H + H^2 + H^3 + ... = H/(1-H) #
We can do this as #0 < H < 1 #
#=> E(X) = HT* d/(dH) ( H/(1-H) ) #
We can find the derivative using the quotient rule:
#y = u/v -> y' = ( vdu - udv )/v^2 #
#d/(dH) ( H/(1-H) ) = 1/(1-H)^2 #
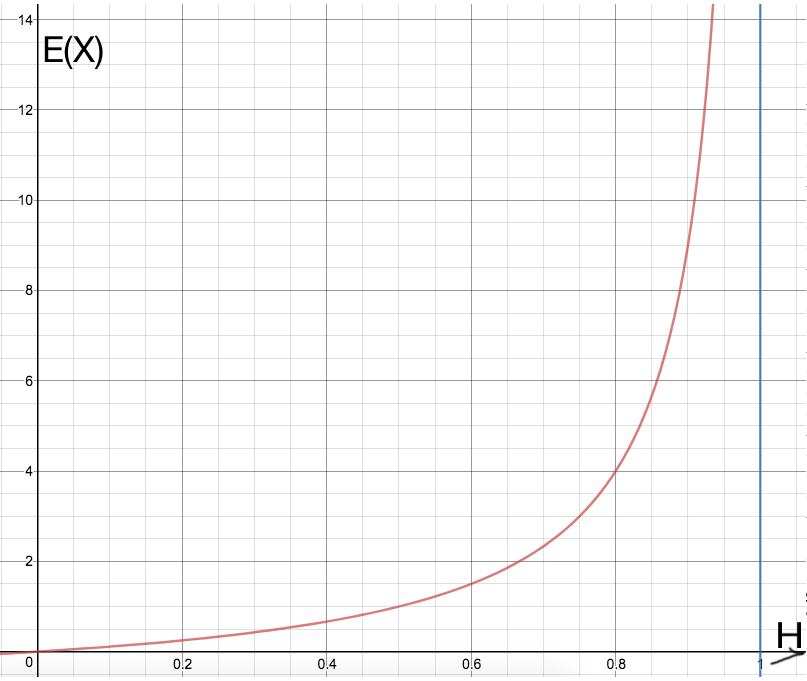
#=> E(X) = (HT)/(1-H)^2 #
We know the total probability is #=1#
#=> H + T =1 #
#=> E(X) = (HT)/(T^2) #
#=> E(X) = H/T #