Question

Question #a1371

Answer 1

We have:

`(1+x^2)y=1-x => y = (1-x)/(1+x^2)`

Differentiating wrt `x` we get:

`dy/dx = ( (1+x^2)(-1) -(1-x)(2x) ) /(1+x^2)^2`
`\ \ \ \ \ \ = ( (-1-x^2) -(2x-2x^2 ) ) /(1+x^2)^2`
`\ \ \ \ \ \ = ( x^2-2x-1 ) /(1+x^2)^2`

Differentiating a second time:

`(d^2y)/(dx^2) = ( (1+x^2)^2(2x-2) - (x^2-2x-1)(2(1+x^2)(2x)) ) /(1+x^2)^4`

`\ \ \ \ \ \ \ \ = ( (1+x^2)(2x-2) - 4x(x^2-2x-1)) /(1+x^2)^3`

At a point of inflection the second derivative vanishes, so we require that `(d^2y)/(dx^2) = 0`, therefore we have:

`(1+x^2)(x-1) - 2x(x^2-2x-1) = 0`

`x+x^3-1-x^2-2x^3+4x^2+2x = 0`

`x^3-3x^2-3x+1 = 0`

By Observation `x=-1` is a root, giving us (by algebraic long division):

`(x+1)(x^2-4x+1) = 0`

So we have:

`x = -1`
`x^2-4x+1 = 0 => (x-2)^2-3 =0 => x=2+-sqrt(3)`

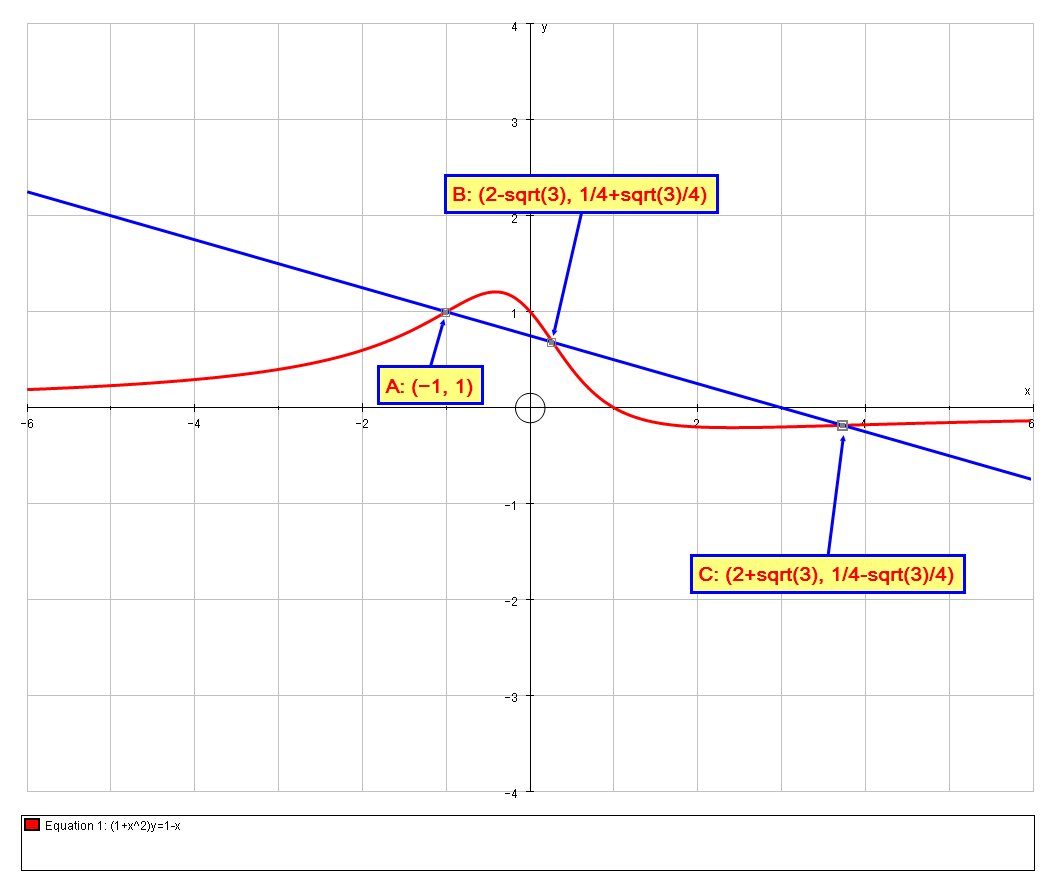
We can calculate the `y`-coordinate and label the points accordingly:

`A=(-1,1)`
`B=(2-sqrt(3), 1/4+sqrt(3)/4)`
`C=(2+sqrt(3), 1/4-sqrt(3)/4)`

The equation of `AB` is:

`y - (1/4+sqrt(3)/4) = (1/4+sqrt(3)/4 - 1)/(2-sqrt(3)+1)(x-(2-sqrt(3)))`
`:. y=3/4-x/4`

And with `x=2+sqrt(3)` we have:

`y=3/4-(2+sqrt(3))/4`
`\ \ =3/4-1/2-sqrt(3)/4`
`\ \ =3/4-1/2-sqrt(3)/4`
`\ \ =1/4-sqrt(3)/4`

So, `C` also lies on `AB`

Hence, there are `3` collinear points of inflection. QED