Question

A cam is to be made to hold a liter of oil. find the radius of the can that will minimize the cost of the metal to make the can.?

Answer 1

`"radius"=10/(root(3)(2pi)` `\ \ \ \ \ \ \ \ \ \`cm

Explanation:

The surface area of a right cylinder is given by:

`S=2pir^2+2pirh`

Where `h` is the height.

The volume of a cylinder is given by:

`V=pir^2h`

We are seeking:

`(dS)/(dr)`

In our surface area equation we have two variables, `r` and `h`. We can't differentiate this ( not with single variable calculus anyway). We need to find `h` in terms of `r`.

We need a volume of 1 litre(`1000"cm"^3`). Using the volume of a cylinder equation:

`1000=pir^2h`

`h=1000/(pir^2)`

Substituting this result in:

`S=2pir^2+2pirh`

`S=2pir^2+2pir(1000/(pir^2))`

`S=2pir^2+2000/r`

We now differentiate this in respect of `r`:

`(dS)/(dr)(2pir^2+2000/(r))=4pir-2000/r^2`

This derivative will allow us to find any stationary points on

`S=2pir^2+2000/(r)`

Equating to zero:

`4pir-2000/r^2=0`

`r^3=1000/(2pi)=> r=10/(root(3)(2pi)`

We don't need to be concerned with complex or negative roots.

We now need to test whether this is a minimum or maximum point. We do this using the second derivative. If:

`f''> 0color(white)(8888)` minimum point.

`f''< 0color(white)(8888)` maximum point.

`(d^2S)/(dr^2)(2pir^2+2000/r)=(dS)/(dr)(4pir-2000/r^2)=4pi+4000/r^3`

Plugging in `r=10/(root(3)(2pi)`

`4pi+4/(10/(root(3)(2pi))^3`

This is positive, so `r=10/(root(3)(2pi))` is a minimum value.

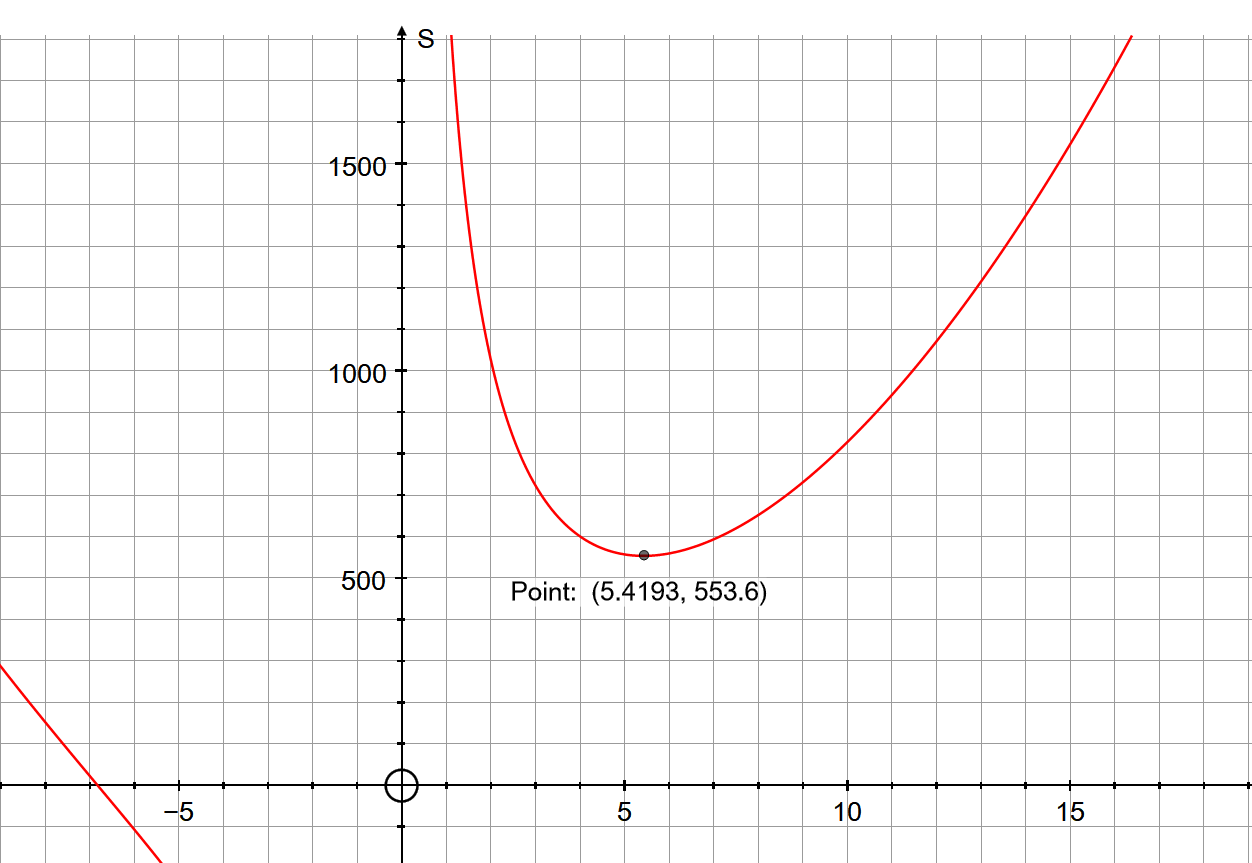
This give a value of `h`:

`h=1000/(pir^2)`

`h=1000/(pi(10/(root(3)(2pi)))^2)=(10(2pi)^(2/3))/pi`

So the can needs to have:

`"radius"=10/(root(3)(2pi))color(white)(8888888)`cm

`"height"=(10(2pi)^(2/3))/picolor(white)(8888)` cm

Graph of `2pir^2+2000/r`