Question

A chain of mass m and length l lies on the surface of a rough sphere of radius R (>l) such that one end of chain is at the top most point of sphere. The chain is held at rest because of friction. What is the gravitational potential energy of the chain?

considering the horizontal diameter of sphere as reference level for gravitational potential energy

Answer 1

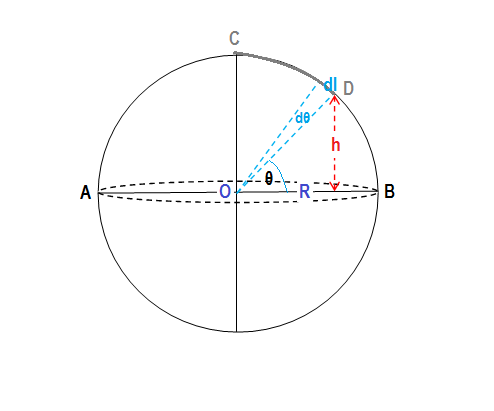
Let the chain of mass `m` and length `l` rests on the sphere along the circumference of the intersecting vertical circle of radius R concentric with the sphere of radius `R`. The chain starts from top position `C` and ends at `D`.

Let the point `D` is at height `h` from the horizontal diameter `AB` taken as reference line for computation of gravitational PE of the chain resting on the sphere as described due to frictional force.

Let the height `h` or arc `BD` subtends angle `theta` at the point `O` ,the center of the sphere as well as the vertical circle.
So `h/R=sintheta=>h=Rsintheta`

Now let us consider a ifinitesimally small chain length `dl` starting at the point `D`. Let it subtends a small angle `d theta` at the center `O`.

So `(dl)/R=d theta=>dl=Rd theta`

The mass of `dl` length of the chain `dm=(mdl)/l`

Now the PE of the small chain length residing at height `h` from the reference line will be given by

`dU=(dm)gh`

`=>dU=(mdl)/lgh`

`=>dU=(mghdl)/l`

`=>dU=(mghR d theta)/l`

`=>dU=(mgR^2sinthetad theta)/l`

Integrating we get the total PE of the chain as

`U=int_theta^(pi/2)(mgR^2sinthetad theta)/l`

`=>U=-(mgR^2)/l[costheta]_theta^(pi/2)`

`=>U=-(mgR^2)/l[cos(pi/2)-costheta]`

`=>U=(mgR^2)/lcostheta`

`=>U=(mgR^2)/lcos(pi/2-l/R)`

`=>U=(mgR^2)/lsin(l/R)`