Question

A great conical mound of height h is built by workers. If the workers simply heap up uniform material found at ground level, and the total weight of the finished mound is M, show that the work they do is (1/4)hM?

Solving it may involve some calculus although i'm not sure about that.

Answer 1

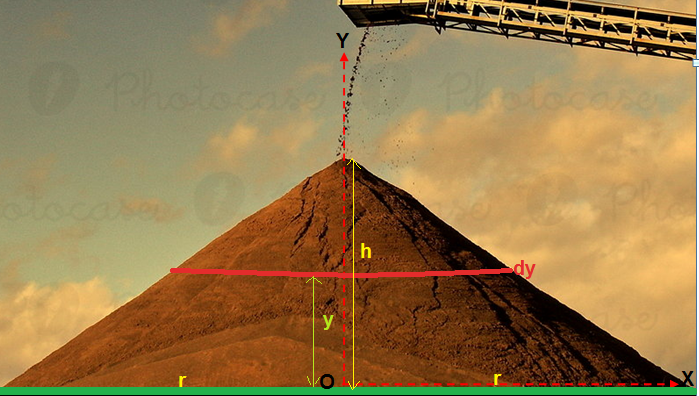
Let the radius of the great conical mound of height `h` built by workers be `r`.

Given that the weight of the finished mound is `M`. So the weight of finished mound per unit volume will be `m=M/(1/3pir^2h)`.

Now for the sake of our calculation let us consider the center of the circular base of the the mound `(O)` as origin with diameter of the mound lying along X-axis and height along Y-axis.

It is obvious that the rate of decrease of radius of the conical mound with height will be given by `r/h`.

Hence at an arbitrary height `y` its radius will be `(r-(ry)/h)=r(1-y/h)`

So the volume of an imaginary circular disk of infinitesimal thickness `dy` at this height `y` will be given by

`dv=pir^2(1-y/h)^2dy`

So weight of this thin disk will be

`=m*dv=M/(1/3pir^2h)*pir^2(1-y/h)^2dy`

`=(3M)/h*(1-y/h)^2dy`

So work done against gravitational pull for lifting this imaginary thin disk to a height of `y` will be given by

`dw="weight"(mdv)xx"height"(y)=(3M)/h*(1-y/h)^2dy*y`

The total work done `W` to finish the mound will be obtained by integrating this `dw` as follows where `y` varies from `0toh`

`W=(3M)/hint_0^h(1-y/h)^2ydy`

`=>W=(3M)/h[y^2/2-(2y^3)/(3h)+y^4/(4 h^2)]_0^h`

`=>W=(3M)/h[h^2/2-(2h^3)/(3h)+h^4/(4 h^2)]`

`=>W=(3M)/h*1/12[6h^2-8h^2+3h^2]`

`=>W=(3M)/h*1/12*h^2`

`=>W=1/4hM`

Proved

Alternative method

Considering the center of mass of the conical mound which is placed at `1/4h` we can calculate the work done in simpler way.

So work done to heap up uniform material found at ground level which is equivalent to lift the COM to a height of `h/4` from ground will be

`W=Mxxh/4=1/4hM`