A ray of light is sent along the line x+y=1 after being reflected from the line y_x=1 it is again reflected from the line y=0 then the equation of the line representing the ray after second reflection may be given as?

1 Answer
Jane
Feb 9, 2018

Here, is a diagram of the whole thing happening,

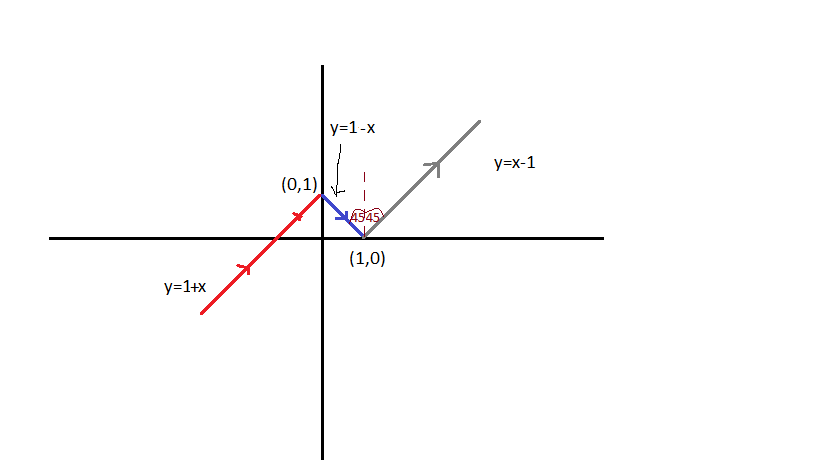
enter image source here

Light after coming by the pathway of #y-x=1# or, #y=1+x# falls on #Y# axis at point #(0,1)# (point of refelection is found as the solution of the given two equations of straight line,as that will be their point of meeting) and then gets refleted via pathway #x+y=1# or, #y=1-x# then falls on #Y=0# i.e #X# axis,and gets reflected as follows,

Now, clearly, slope of the straight line #y-x=1# is 45 degrees, and the reflected ray from the #X# axis will be parallel to that.

So,let the equation of the reflected pathway is #y-x-c=0#

And, that of the straight line,to which it will be parallel is #y=1+x# or, #y-x-1=0#

Now,if the distance between them is #d# , we know, #d= (|c1 +c2|)/sqrt(a^2+b^2)# for two straight lines #ax+by+c1=0# & #ax+by+c2=0#

here, #a=1 ,b=1# and #d=sqrt(1^2 +1^2)=sqrt(2)#

#d= (|1-c|)/sqrt(2)#

So, #c=-1#

So,the equation of straight line,alomg which the reflected ray will go, will be #y-x+1=0# or, #y=x-1#

Related questions
Impact of this question
2516 views around the world
You can reuse this answer
Creative Commons License