Question

A study of one thousand teens found that the number of hours they spend on social networking sites each week normally distributed with a mean of 15 hours. The population standard deviation is 2 hours. What is the 95% confidence interval for the mean?

Answer 1

Population Mean lies between `15.0294` and `14.9706`

Explanation:

Given -

Sample Mean `barx=15`
Sample size `n=1000`
Population SD `sigma=2`
Confidence interval `= 95%`

Population Mean `mu=barx+-(z xx SE)`

`SE ->` Standard Error

`SE=sigma/sqrtn=15/1000=0.015`

Critical Value of `z` for 95% confidence interval `=1.96`

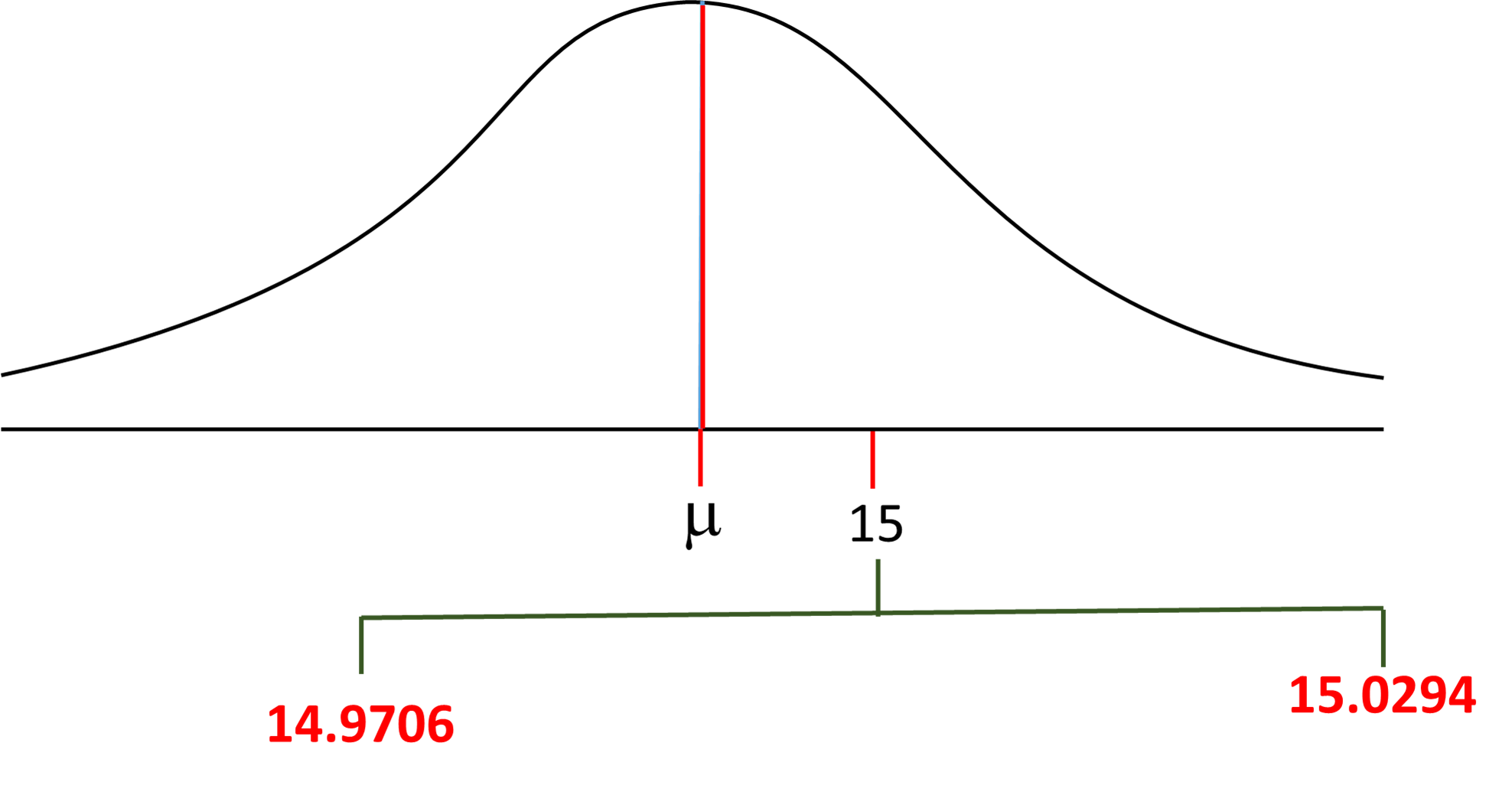
`mu=15+-(1.96 xx 0.015)`
`mu=15+-0.0294`

Upper Limit

`mu=15+0.0294=15.0294`

Lower Limit

`mu=15-0.0294=14.9706`