An object is traveling around a circle with a radius of 2 meters. If in 20 seconds the object travels 5 meters, what is its angular speed? What is its linear speed?

1 Answer
Gió
Jan 29, 2016

I found #0.25m/s# and #0.125"rad/s"#.

Explanation:

The linear speed will be:
#v="distance"/"time"=5/20=0.25m/s#
The angular speed is:
#omega="angle"/"time"=theta/t#
but...how do we find the angle described by our object????
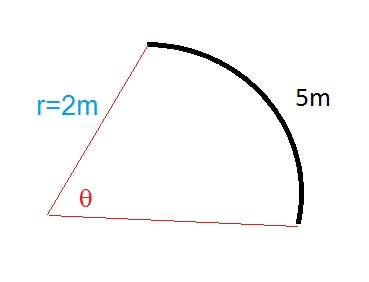
enter image source here
We know that between radius, #r#, angle #theta# (in radians) and arc length #s# there is a relationship as:
#s=rtheta#
so #theta=s/r=5/2#rad
Finally then:
#omega=(5/2)/20=0.125"rad/s"#

The two speeds are also connected through the radius as:
#v=omega*r#...try it!!! :-)

Related questions
Impact of this question
26072 views around the world
You can reuse this answer
Creative Commons License