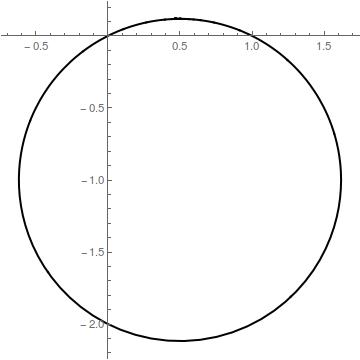
Consider a family of lines #(4a+3)x -(a+1)y-(2a+1)=0# where #ainR#?

Question

A) The locus of the foot of the perpendicular from the origin on each member of this family is?
B) A member of this family with positive gradient making an angle of #pi/4# with the line #3x-4y=2# is?
C) Minimum area of triangle which a member of this family with negative gradient can make with the positive semi axes is?

971 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-09T14:24:20

See below.

#(4a+3)x -(a+1)y-(2a+1)=0# can be represented as

#L-><< p-p_0, vec v >> = 0#

with

#p = {x,y}#
#vec v = {4a+3,-(a+1)}#
#p_0 = {0,-(2a+1)/(a+1)}#

Now the perpendicular line to #L# passing by the origin of coordinates is

#L_p-> p=lambda vec v# Now substituting into #L#

#<< lambda vec v-p_0, vec v >> = lambda norm(vec v)^2- << p_0, vec v >> = 0# and then

#lambda = << p_0, vec v >>/norm(vec v)^2# and the point of intersection #L nn L_p# is given by

#p_i = << p_0, vec v >>/norm(vec v)^2 vec v# giving the locus

#p_i(a) = (2a+1)/(17a^2+26a+10){4a+3,a+1}#

so

#(A)->(2a+1)/(17a^2+26a+10){4a+3,a+1}#

enter image source here