Question

Consider the molecule [MnX6]2+, where X is a neutral ligand. Assume that X is a strong field ligand?

Answer 1

DISCLAIMER: Long answer!

`A)`

THE NUMBER OF 3D VALENCE ELECTRONS IN THE COMPLEX

When you examine the location of `"Mn"` on the periodic table, you should find that the electron configuration ends in `4s^2 3d^5`.

Since `"X"` is stated to be a neutral ligand, `"Mn"` in `["MnX"_6]^(2+)` by charge conservation is a `+2` oxidation state. Therefore, we doubly ionize neutral manganese to obtain the electron configuration `3d^5`, removing the two `4s` electrons first.

HIGH-SPIN VS LOW-SPIN, AS IT RELATES TO STRONG-FIELD AND WEAK-FIELD LIGANDS

A `d^5` metal such as this can form either a high-spin or low-spin complex, depending on the crystal field strength of the ligand.

We assume strong-field for `"X"`, which means that it can either be:

• A `sigma` donor (such as `:"NH"_3`, `"CO"`, or `""^(-)"CN"`)
• A `pi` acceptor (such as `"CO"` or `""^(-)"CN"`)
• Both (such as `"CO"` or `""^(-)"CN"`)

SIGMA DONORS

Let's say we just have a good `sigma` donor.

In this case, it destabilizes the `e_(g)` orbitals (there are two of those orbitals), since those interact with the `sigma` bonding molecular orbitals brought in by the `sigma` donor(s). `"CO"` is an example:

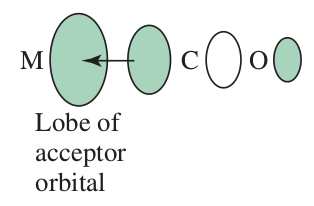
As a result, the two upper-energy (`e_g`) orbitals get higher in energy (relative to the free-ion energy), increasing the crystal-field splitting energy `Delta_o` (`Delta` in your diagram), promoting low spin.

PI ACCEPTORS

Or, let's say we have a good `pi` acceptor.

In this case, the `pi` antibonding molecular orbitals of the ligand accept electrons from the `3` lower-energy (`t_(2g)`) `3d` orbitals.

This stabilizes these `3` lower-energy (`t_(2g)`) `3d` orbitals, decreasing their energy. This also increases `Delta_o`.

Since `"CO"` is both, it is one of the strongest-field ligands there is.

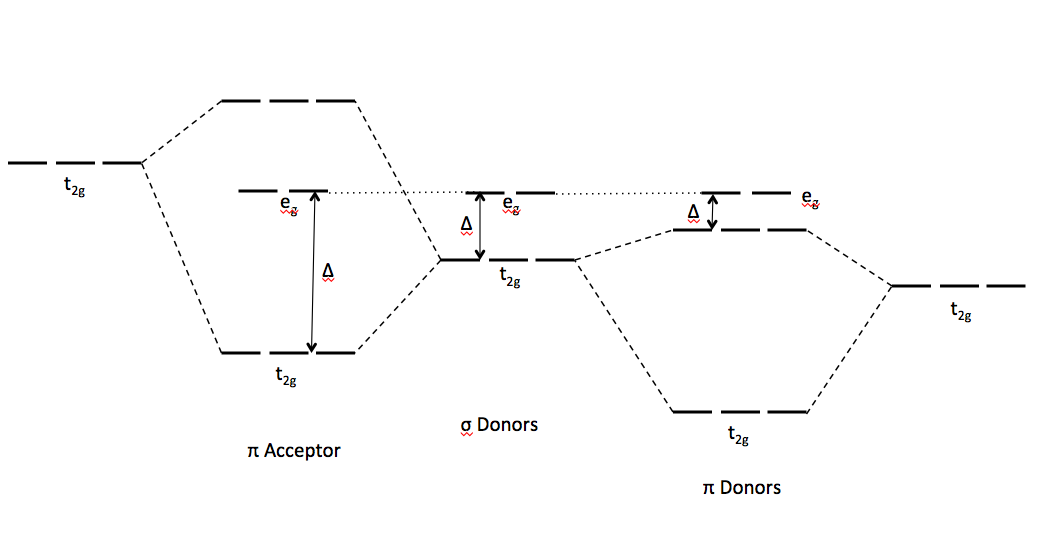
CRYSTAL-FIELD SPLITTING DIAGRAM

When a transition metal complex has a coordination number of `6` (given that it has six `"X"` ligands bound to it), it forms an octahedral electron geometry.

The diagram you were given is the crystal-field splitting diagram for the five `3d` orbitals of manganese once the manganese(II) complex is placed into an octahedral field that splits its `d`-orbital energies.

Here is the filled diagram for a manganese(II) complex in high spin or low spin:

The difference is that for a low spin complex, which corresponds to having a strong-field ligand, `Delta_o` is large.

So the electrons can capably fill the `3` lower-energy `t_(2g)` orbitals first... before they can feasibly fill the `2` higher-energy `e_g` orbitals.

`B)`

PI DONORS

A weak-field ligand contributes little repulsion. Actually, weak-field ligands are typically `pi` donors, and weak `sigma` donors.

If you have a `pi` donor, such as any halide (`"Cl"^(-)`, `"F"^(-)`, etc):

It has filled `pi` bonding molecular orbitals that donate into the three (`t_(2g)`) `3d` orbitals and destabilize them, increasing their energy.

That actually decreases `Delta_o`, and promotes high spin.

So, `Delta_o` would be smaller for a weaker-field ligand.

This diagram summarizes the trends for `pi` acceptors, `sigma` donors, and `pi` donors:

`C)`

CRYSTAL-FIELD SPLITTING ENERGY

Since the light absorbed will promote electrons from the `t_(2g)` into the `e_g` orbitals, the size of `Delta_o` tells you how much energy this light frequency corresponds to.

Since `Delta_o` becomes smaller when switching to a weaker-field ligand, and `Delta_o prop E prop nu`, a smaller frequency of light can be absorbed than before.

(Thus, you can also say that a longer wavelength is absorbed.)