Consider the plane 3x-7y-z+7=0 a) State any point on the plane b) State any direction vector of the plane c)is the point (-2,-1,8) on the plane?

3 Answers
Narad T.
Dec 1, 2017

#(a)# The point #(0,0,7)# is on the plane. #(b)#The vector # <1,1,-4># is on the plane. #(c)#The point #(-2,-1,8)# is on the plane.

Explanation:

The plane is

#3x-7y-z+7=0#

Let #(x,y)=(0,0)#

Then

#(3xx0)-(7xx0)-z+7=0#

so,

#z=7#

Therefore,

The point #(0,0,7)# is on the plane

A vector perpendicular to the plane is #vec n=<3, -7, -1># which are the coefficients of #x#, #y# and #z#

So any vector #vecu=<a,b,c># will lie on the plane iif

The dot product #=0#

#vecn.vecu=<3, -7, -1> . < a ,b,c > =3a-7b-c=0#

If #a=1# and #b=1#, then #c=3*1-7*1=-4#

The vector #vecu= <1,1,-4># is on the plane

The point #(-2,-1,8)#

Plug in the point in the equation of the plane

#3x-7y-z+7=3*(-2)-7(-1)-8+7=-6+7-8+7=0#

Therefore,

The point #(-2,-1,8)# is on the plane

Somebody N.
Dec 1, 2017

See below.

Explanation:

a). Since #3x-7y-z+7=0# is the equation of the plane, we can find points in the plane by assigning arbitrary values to say x and y and then calculating the value of z.

Let #x=1# and #y=1#

Then:
#3(1)-7(1)-z+7=0=>z=3#

point: #((1),(1),(3))#

b). Find any two point in the plane. We already have one from the last answer. A second point could be.

Let: #x=2# and #y=3#

#3(2)-7(3)-z+7=0=>z=-8#

point: #((2),(3),(-8))#

Create vector:

#A=((1),(1),(3))#

#B=((2),(3),(-8))#

Vector AB:

#vec(AB)=((2),(3),(-8))-((1),(1),(3))=((1),(2),(-11))#

3).

If point #(-2 ,-1 , 8)# lies in the plane, the it will satisfy the equation:

#3x-7y-z+7=0#

#3(-2)-7(-1)-(8)+7=0#

#-6+7-8+7=0#

#0=0#

So #(-2 ,-1 , 8)# lies in the plane.

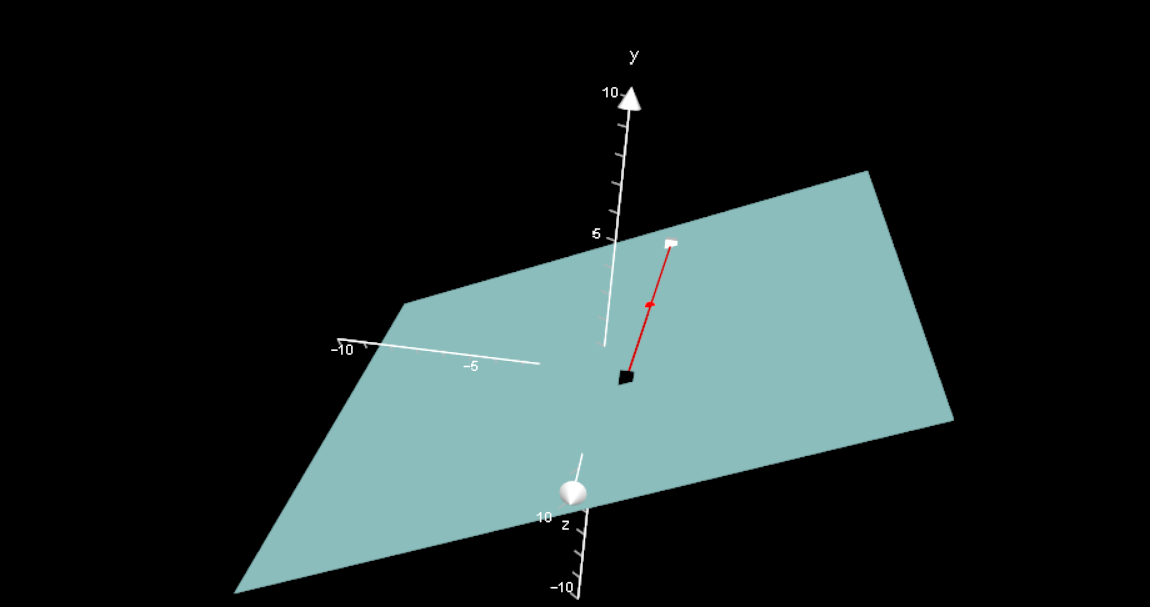
On the graph, A is the black point and B is the white point, with the vector #vec(AB)# connecting them.

enter image source here

Steve M
Dec 1, 2017

a) #P(0,0,7)# lies on the plane.
b) #<< 1,0,3 >> # lies on the plane
c) #(-2,-1,8)# lies on the plane

Explanation:

a) Any point #(x,y,z)# will lie on the plane provided #x#, #y# and #z# satIsfy the plane equation. Arbitrarily choose #x=0# and #y=0# then we require:

# 3(0) -7(0) -z+7=0 => z=7#

Hence #P(0,0,7)# lies on the plane.

b) Let us find another point on the plane, Arbitrarily choose #x=1# and #y=0# then we require:

# 3(1) -7(0) -z+7=0 => z=10#

So #Q(1,0,10)# lies on the plane. and therefore the vector #bb(vec(PQ))# and:

# bb(vec(PQ)) = bb(vec(OQ))- bb(vec(OP)) #
# \ \ \ \ \ \ = << 1,0,10 >> - << 0,0, 7 >> #
# \ \ \ \ \ \ = << 1,0,3 >> #

Hence #<< 1,0,3 >> # lies on the plane

c) If we substitute the coordinates #(-2,-1,8)#into the equation of the plane we find:

# LHS = 3(-2) -7(-1) -8+7= -6 +7-8 +7 = -0#

Hence #(-2,-1,8)# lies on the plane

Related questions
Impact of this question
709 views around the world
You can reuse this answer
Creative Commons License