Question

Determines the volume that originates the surface bounded by the parabola and the line when turning around the axis Y?

determines the volume that originates the surface bounded by the parabola `y + x^2 = 0` and the line `y + 4 = 0` when turning around the axis Y

Answer 1

`V_("Solid")=8pi`

Explanation:

.

`y+x^2=0, :. y=-x^2` This is a parabola opening down.

`y+4=0, :. y=-4` This is a horizontal line.

Let's find the intersections of the line with the parabola:

`-x^2=-4, :. x=+-2`

Let's see what the area looks like:

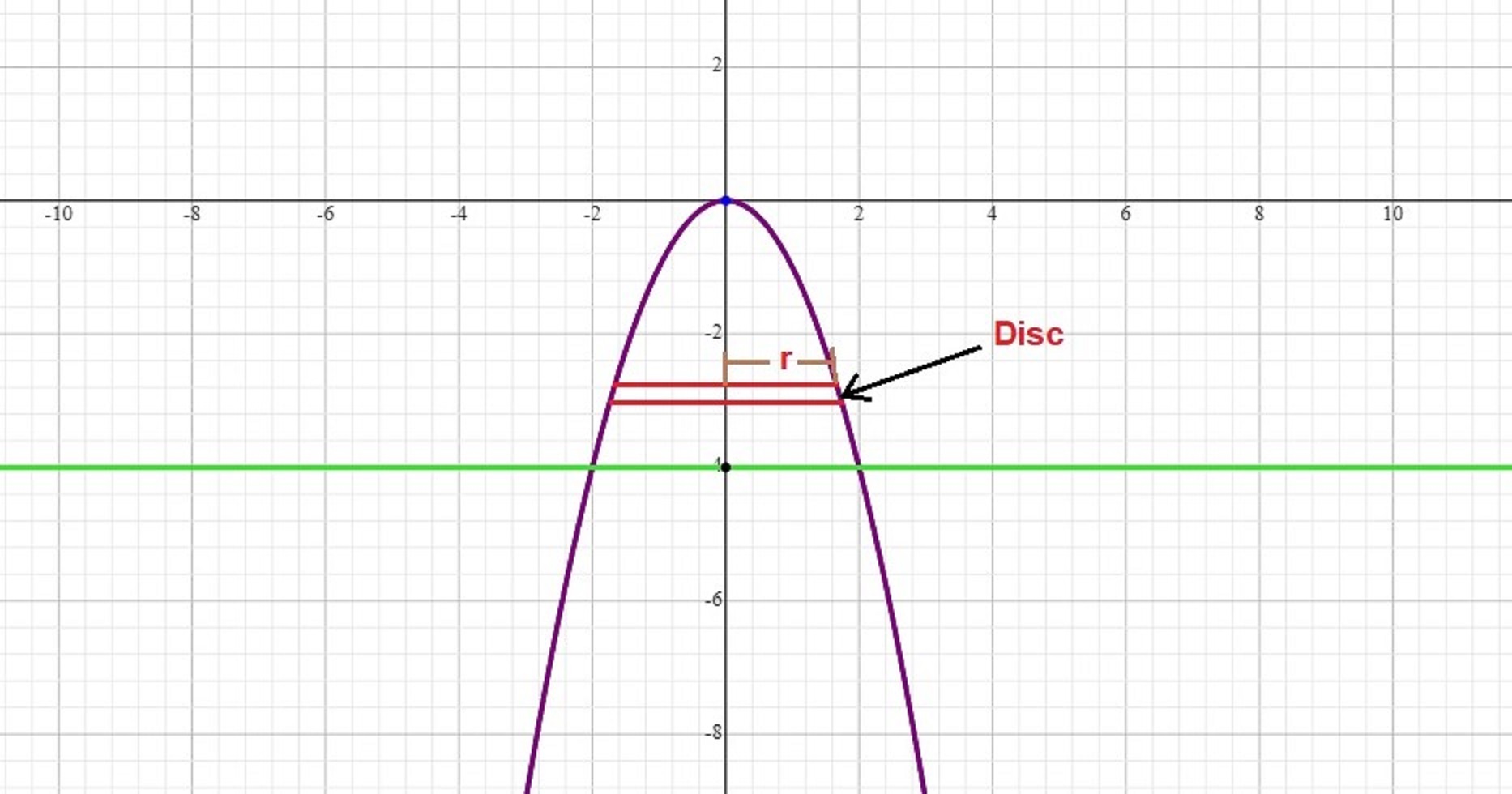
The parabola is shown in purple.

The horizontal line is shown in green.

The area bounded by these two curves is rotated around the `y`-axis.

If we envision a cross-section (slice), perpendicular to the `y`-axis, of the volume generated it would look like a disc with a thickness of `dy` as shown.

If we take the equation of the parabola and solve for `x` we get the equation expressed in the form of #`x` as a function of `y`:

`x=+-sqrt(-y)`

The radius of the disc is `r=x=sqrt(-y)`.

The area of the disc is `A=pir^2=-piy`

The volume of the disc is `V=-piydy`

If we now imagine that the thickness of this disc, i.e. `dy` is infinitely small we can say that the volume generated is the sum of the volumes of infinite number of such discs whose radius is equal to `x` which is a function of `y` and varies from `0` to `2`.

To add these volumes together, we take the integral of the volume function for the disc and evaluate it between `y=0 and -4`:

`V_("Solid")=int_(-4)^0-piydy=-piint_(-4)^0ydy=(-piy^2/2)_(-4)^0=0-(-8pi)=8pi`