Question

Evaluate (-1)^1/10 using De Moivre's theorem?

Answer 1

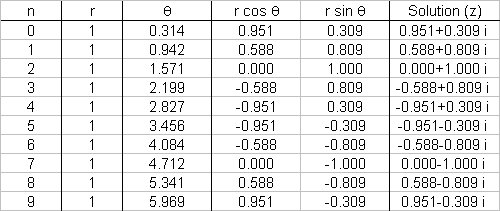
Explanation:

We seek:

`root(10)(-1)`

Let `omega=-1`, and let `z^10 = omega` so that `z = root(10)(-1)`

First, we will put the complex number, `omega`, into polar form, which we can calculate directly:

`omega = cos(pi) + isin(pi)`

We now want to solve the equation `z^10=omega` for `z` (to gain `10` solutions):

`z^10 = cos(pi) + isin(pi)`

Whenever dealing with complex variable equation such as this it is essential to remember that the complex exponential (and therefore the polar representation) has a period of `2pi`, so we can equivalently write (incorporating the periodicity):

`z^10 = cos(pi+2npi) + isin(pi+2npi) \ \ \ n in ZZ`

By De Moivre's Theorem we can write this as:

`z = (cos(pi+2npi) + isin(pi+2npi))^(1/10)`
`\ \ = cos((pi+2npi)/10) + isin((pi+2npi)/10)`
`\ \ = cos(theta) + isin(theta)`

Where:

`theta = (pi+2npi)/10 = ((2n+1)pi)/10`

And we will get `10` unique solutions by choosing appropriate values of `n`. Working to 3dp, and using excel to assist, we get:

After which the pattern continues (due the above mentioned periodicity).

We can plot these solutions on the Argand Diagram: