Question

find a point on the graph of the given function where the tangent or normal line satisfies the indicated condition, and then write an equation for this line.?

Answer 1

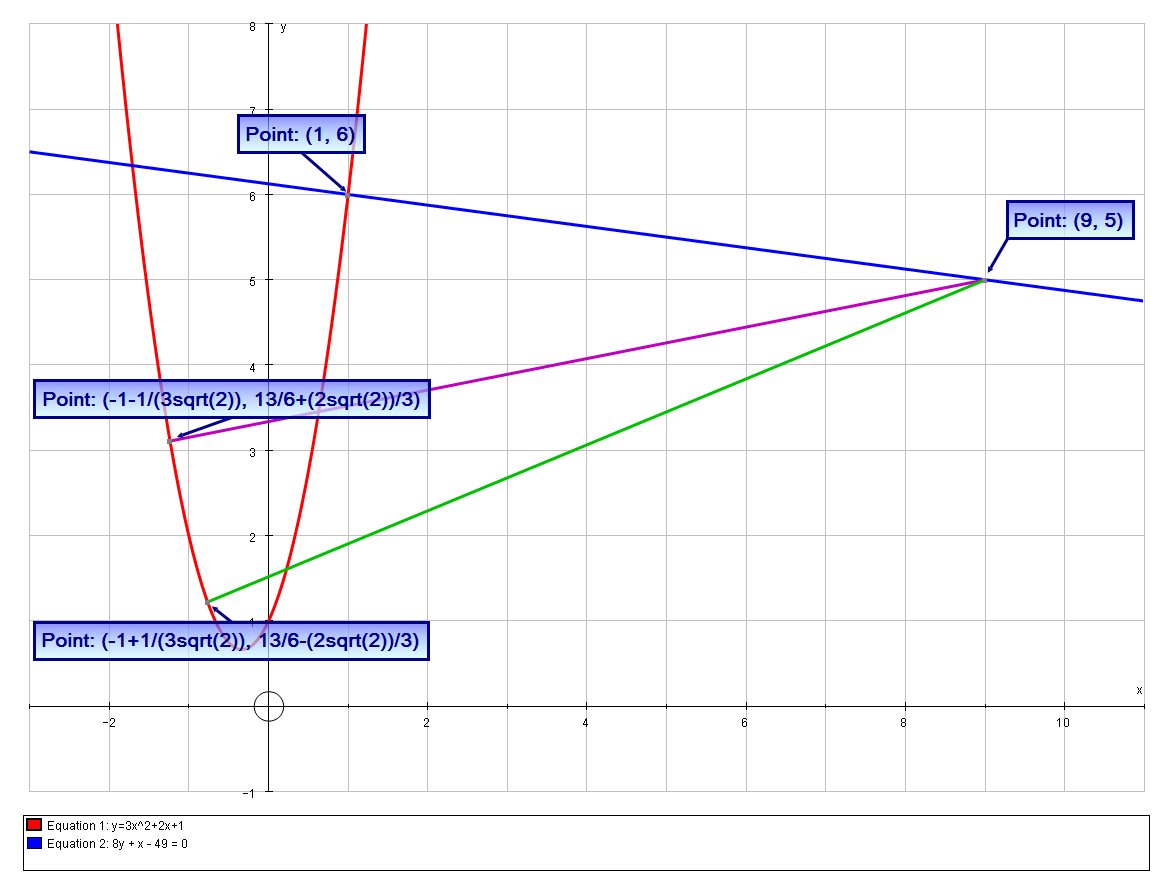
There are three possible coordinates:

`( 1, 6 ) ; ( -1-1/(3sqrt(2)), 13/6+(2sqrt(2))/3 ) ; ( -1+1/(3sqrt(2)), 13/6-(2sqrt(2))/3 )`

If we choose `(1,6)` then the normal equation is:

`8y + x - 49 = 0`

Explanation:

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is `−1`).

We have:

`f(x) = 3x^2+2x+1`

Differentiating wrt `x` we get

`f'(x) = 6x+2`

Suppose the point we seek has coordinates `P(a,b)`, then as `P` lies on our given curve we have:

`b = 3a^2+2a+1` ..... [A]

The slope of the tangent line at `P` is given by:

`m_T = f'(a) = 6a+2`

So, the slope of the normal line is given by:

`m_N = -1/(6a+2)`

As the normal also passes through `(9,5)` the equation of the normal using the point/slope form `y-y_1=m(x-x_1)` is;

`y - 5 = -1/(6a+2)(x-9)` ..... [B]

This normal equation also passes through the point `P` on the curve, and so:

`b - 5 = -1/(6a+2)(a-9)`

Substituting [A] gives us:

`3a^2+2a+1 - 5 = -(a-9)/(6a+2)`
`:. (6a+2)(3a^2+2a- 4) = -a+9`
`:. 18a^3+12a^2- 24a + 6a^2+4a- 8 = -a+9`
`:. 18a^3+18a^2- 19a -17 = 0`

The challenge is to now solve this cubic for `a`. Fortunately, by observation, we see that `a=1` is a solution, hence by the factor theorem, `(x-1)` is a factor and thus we can can perform algebraic long division to form linear and quadratic factors, giving:

`(a-1)(18a^2+36a+17) = 0`

Then using the quadratic formula, we gain the additional roots, and so we have:

`a=1, -1+-1/(3sqrt(2))`

Using [A] with these values of `a` we get the corresponding values of `b`:

`a= { (1), (-1-1/(3sqrt(2))), (-1+1/(3sqrt(2))) :} => b= { (6), (13/6+(2sqrt(2))/3), (13/6-(2sqrt(2))/3) :}`

Hence there are three possible coordinates:

`( 1, 6 )`
`( -1-1/(3sqrt(2)), 13/6+(2sqrt(2))/3 )`
`( -1+1/(3sqrt(2)), 13/6-(2sqrt(2))/3 )`

If we choose `(1,6)` then using [B] the normal equation is:

`y - 5 = -1/(6+2)(x-9)`
`:. 8y - 40 = -x+9`
`:. 8y + x - 49 = 0`

We can confirm this graphically: