Find speed in Km/Hr ?
Percy standing in the midst of a field observes a flying bird in his north at an angle of elevation of #30^@# and after #2min# he observes the bird in his south at an angle of elevation of #60^@# . If the birdflies in a straight line all along at a height of #50sqrt3m# , then find its speed in kilometer per hour.
Percy standing in the midst of a field observes a flying bird in his north at an angle of elevation of
1 Answer
Dec 11, 2017
Explanation:
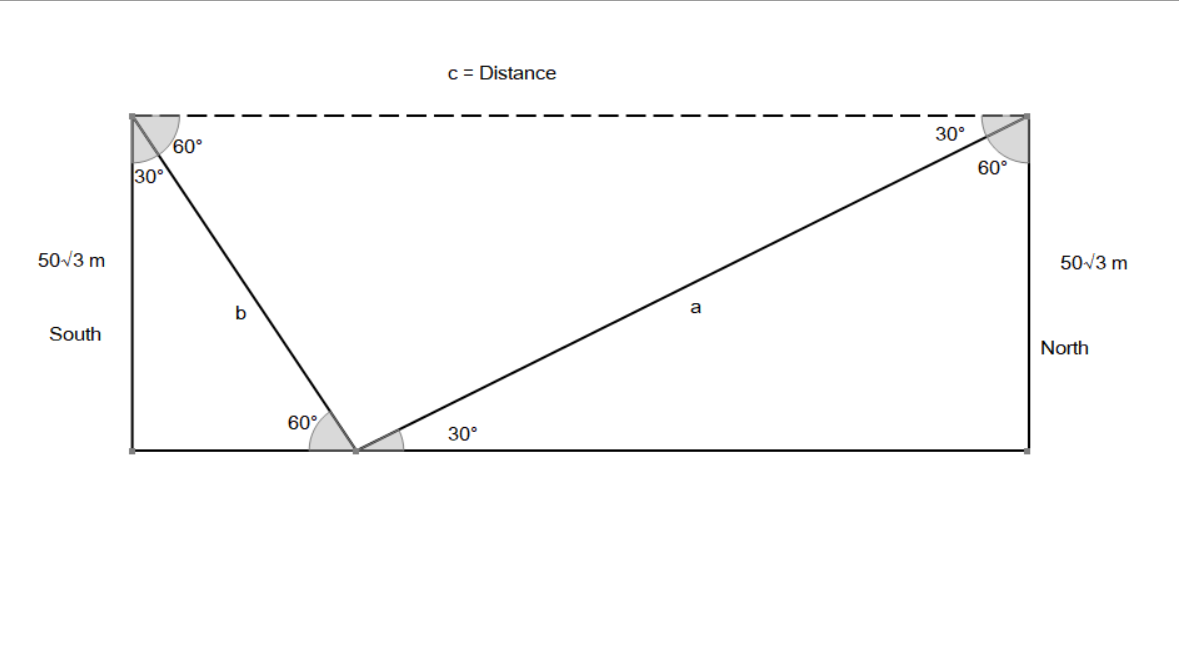
From the diagram we need to find distance c. Using Pythagoras' theorem
Distance travelled/ time taken = speed

