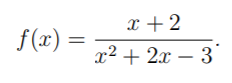the graph #f(x) = (x+2)/(x^2+2x-3)# has #2# points of discontinuity.
if calculating #f(x)# involves division by #0#, then #f(x)# cannot be defined.
this happens for the values of #x# at which #x^2+2x-3 = 0#.
#x^2+2x-3 = 0# can be factorised:
#x^2 + 2x - 3 = (x+3)(x-1)#
and solved as a quadratic equation:
#(x+3)(x-1) = 0#
#x + 3 = 0# or #x - 1 = 0#
#x = -3# or #x = 1#
this means that at #x = -3# and #x = 1#, #f(x)# is not defined, and so there is a discontinuity in the graph.
neither point of discontinuity has a limit.
take #x = -3:#
#x = -4 rarr f(x) = -2/7#
#x = -3.5 rarr f(x) = -2/3#
#x = -3.25 rarr f(x) = -1.176#
as #x# approaches #-3# from the left, it decreases at a faster rate until #f(x)# reaches minus infinity #-oo#.
#x = -2 rarr f(x) = 0#
#x = -2.5 rarr f(x) = 0.286#
#x = -2.75 rarr f(x) = 0.8#
as #x# approaches #-3# from the right, it increases at a faster rate until #f(x)# reaches infinity #oo#.
since the value of #f(x)# takes two different values if approached from the left and from the right, the limit of #f(x)# as #x# approaches #-3# cannot be stated.
the same is true for the graph at #x = 1#; if approaching #x# from the left, #f(x)# decreases to #-oo#, while when approaching #x# from higher values on the right, #f(x)# increases to #oo#.