How do you simplify it??
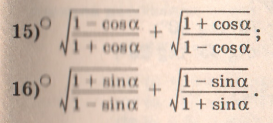
2 Answers
Please see a Proof of Ex. 15 in the Explanation.
Explanation:
Let us solve Ex. 15.
We will use these Identities :
Method 1 :
Method 2 :
Ex. 16 can be proved in the similar fashion.
Since, the L.H.S. is non-negative, so has to be the
R.H.S.
Explanation:
I'm geeky enough to recognize these forms as associated with the tangent half angle formulas.
The first stem from the cosine double angle formula:
These provide a nice way to change 1 plus or minus cosine to twice the square of the trig function of a half angle. It's easier in symbols:
We get
I always get concerned when the absolute value appears. But w're after the sum of principal values, positive numbers, so let's go with it.
The tangent and its reciprocal have the same sign so we can bring them together like this:
Wow, that simplified.
Let's check it. Let's see what the Socratic grapher does with it. We'll plot
graph{sqrt((1-cos x)/(1 + cos x)) + sqrt((1 +cos x)/( 1 - cos x ) ) - | 2 csc x| [-0.00782, 0.007924, -0.0003786, 0.0004086]}
That's zero, though it does get hinky around the singularities at
Gotta go, can't do the other one right now.

