Question

If S is a set with 10 elements and A is subset of S, what is the probability that A has 3 or more elements?

Answer 1

`0.8`

Explanation:

`A sub S`

if `S` has `10` elements, `A` must have `10` elements or less.

assuming that `A` has at least `1` element, it can have `1,2,3,4,5,6,7,8,9` or `10` elements.

'`1,2,3,4,5,6,7,8,9,10`' means that there are `10` possible numbers of elements that `A` could have.

in the same way, there are `8` ways of having at least `3` elements
(`3,4,5,6,7,8,9,10`).

probability = no. of possible outcomes specified / total no. of outcomes

`8/10 = 0.8`

the probability of having `3` or more elements is `0.8`

Answer 2

If the elements are indistinguishable, `8/11=0.bar(72)`. If distinguishable, `121/128~~0.9453`

Explanation:

The answer depends on the nature of the elements inside the sets.

If the elements are indistinguishable, so that we are solely looking at the number of things inside the set (so the elements being black marbles and the set being a bag - we can have 0 marbles in there, or 1, or 2, etc, all the way up to 10 - and so 11 possible conditions of the bag). In this way, it's only when there are less than 3 marbles in the bag that the condition fails. And so we have as a probability:

`8/11`

If the elements are distinguishable, such as 10 different scrabble letters and that same black bag - now we have a new element to account for in that black bag - while there is one way to have 0 items in there (i.e. it's empty), there are 10 ways to put 1 letter into the bag, 45 to put in 2, etc...

So we have to look to a summation of the different combinations (10 choose 3, 10 choose 4, etc... up to 10 choose 10). We can do that by summing up the relevant line and elements of Pascal's Triangle:

`120+210+252+210+120+45+10+1=968`

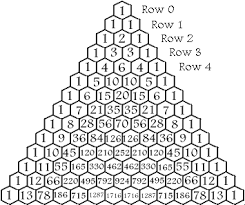
We divide this by what we've added up so far and add to it 10 choose 0, 10 choose 1, and 10 choose 2:

`968+1+10+45=1024`

Giving:

`968/1024=121/128~~0.9453=94.53%`