In the motion called precession of the equinoxes, the Earth's axis of rotation precesses about the perpendicular to its orbital plane with a period of 2.58 104 yr. How would you calculate the torque on the Earth that is causing this precession? ?
The angular momentum vector of a precessing gyroscope sweeps out a cone as shown in the figure below. The angular speed of the tip of the angular momentum vector, called its precessional frequency, is given by #ωp = τ/L# , where #τ# is the magnitude of the torque on the gyroscope and #L# is the magnitude of its angular momentum. 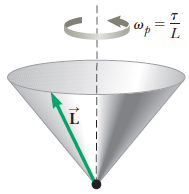
The angular momentum vector of a precessing gyroscope sweeps out a cone as shown in the figure below. The angular speed of the tip of the angular momentum vector, called its precessional frequency, is given by 
1 Answer
Torque :
Explanation:
Torque is defined as the rate at which the angular momentum vector changes.
In the case of Earth's gyration, the angular momentum's magnitude remains the same and only its direction changes due to the torque.
The angular momentum vector
If
If
where
So the magnitude of the torque is :
One can write the spin angular momentum in terms of the moment-of-inertia (
The angular frequencies of spin and precession can be written in terms of the the spin time period and precession time period as :
Numerical Evaluation:

