Question

Please answer the given question?

Answer 1

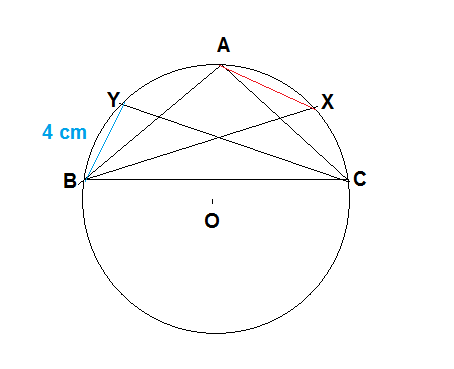
Given that in `DeltaABC,AB=AC`

`BX and CY` are bisectors of `/_ ABC and /_ ACB` respectively.
So `/_ ABC= /_ ACB`
`BY=4cm`, we are to find out length of `AX`

we have

`/_ ABC = /_ ACB`
`=>1/2/_ ABC = 1/2 /_ ACB`

`=>/_ ABX=/_ BCY`

( since `BX and CY` are bisectors of `/_ ABC and /_ ACB` respectively )

As we have `=>/_ ABX=/_ BCY`, the two circumferential equal angles of same circle, the length of the arcs on which these angles stand will be same .

Hence `arcBY=arcAX` and so chord`AX=`chord `BY=4cm`