Question: find a general solution of homogeneous linear difference equation of the 2nd order with constant coefficients. How to solve it? Thank you. (pictures below)
task:
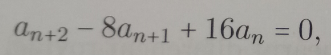
this should be solution:
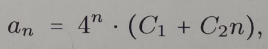
Thank you!
task:
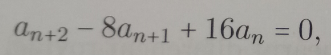
this should be solution:
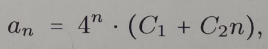
Thank you!
1 Answer
# a_n = 4^n(An+b) #
Explanation:
We seek a solution to the Linear difference equation:
# a_(n+2) -8_(n+1) + 16a_n = 0 # ..... [A]
This is a Second Order Homogeneous linear difference equations, and is solved in a similar way to a second order linear differential equations with constant coefficients, by forming the Auxiliary Equation, which is the polynomial equation with the coefficients of the difference terms:
So, the associated Auxiliary equation is:
# m^2-8m+16 = 0#
# :. (m-4)^2 = 0 #
And so we have the solutions:
# m = +-4 # (repeated real root)
The roots of the auxiliary equation determine parts of the solution, which if linearly independent then the superposition of the solutions form the full general solution.
- Real distinct roots
#m=alpha,beta, ...# will yield independent solutions of the form#a_alpha=Aalpha^n# ,#a_beta=Bbeta^n# , ... - Real repeated roots
#m=alpha# , will yield a solution of the form# a_n=(An+B)alpha^n# where the polynomial has the same degree as the repeat. - Complex roots (which must occur as conjugate pairs)
#m=R(costheta+isintheta)# will yield solutions of the form# a_n=R^n(Acost theta n+Bsin theta n)#
Thus the General Solution of the homogeneous equation [A] is:
# a_n = 4^n(An+b) \ \ \ \ # QED

