Question: Find the particular solution #y_p(x)# of homogeneous linear equation of the 2. order with constant coefficients. How do I solve it? Thank you! (pictures below)
here:
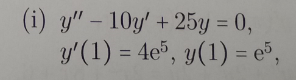
this should be solution:
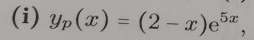
here:
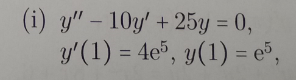
this should be solution:
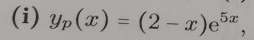
2 Answers
Solve the characteristic equation:
so we have a single root with double multiplicity:
In such case the general solution of the equation is:
Evaluate the first derivative:
and determine the constants from the initial conditions:
Then the required solution is:
# y = (2-x)e^(5x) #
Explanation:
We seek a solution to
# y'' + 10y' +25y = 0# with#y'(1)=4e^5, y(1)=e^5# ..... [A]
This is a second order linear non-Homogeneous Differentiation Equation with constant coefficients. The standard approach is to find a solution,
Complementary Function
The homogeneous equation associated with [A] is
# y'' + 10y' +25y = 0 # ..... [B]
And it's associated Auxiliary equation is:
# m^2 +10m +25 = 0 => (m+5)^2=0#
And so we have the solutions:
# m = +-5 \ \ \ \ # (repeated real)
The roots of the auxiliary equation determine parts of the solution, which if linearly independent then the superposition of the solutions form the full general solution.
- Real distinct roots
#m=alpha,beta, ...# will yield linearly independent solutions of the form#y_1=Ae^(alphax)# ,#y_2=Be^(betax)# , ... - Real repeated roots
#m=alpha# , will yield a solution of the form#y=(Ax+B)e^(alphax)# where the polynomial has the same degree as the repeat. - Complex roots (which must occur as conjugate pairs)
#m=p+-qi# will yield a pairs linearly independent solutions of the form#y=e^(px)(Acos(qx)+Bsin(qx))#
Thus the General solution of the homogeneous equation [B] is:
# y = (Ax+B)e^(5x) #
Note this solution has
Now, we form the first derivative using the product rule
# y' = (Ax+B)(5e^(5x)) + (A)(e^(5x)) #
# \ \ \ \= (5Ax+5B+A)e^(5x) #
and applying the initial conditions:
# {: (y(1)=e^5, => (A+B)e^(5) = 4^5, => A+B =1), (y'(1)=4e^5, => (5A+5B+A)e^(5) = 4e^5, => 6A+5B=4 ) :} #
And solving simultaneously we get the solution:
# A=-1# and#B=2 #
Thus we the the Particular Solution:
# y = (-x+2)e^(5x) #
# :. y = (2-x)e^(5x) \ \ \ # QED


