Simplifying #S_(k+1)# completely. Thanks?!!
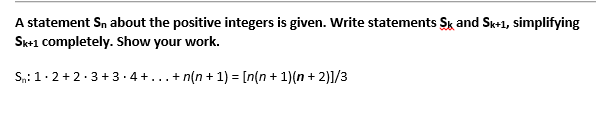
2 Answers
Explanation:
Can't we just substitute
The sequence is:
So, if we want to calculate
In the case of
If we want to expand this, it becomes
Explanation:
Let the statement be true for n=k,
Let us verify for
n=k+1, then
Thus,
Verified.
Thus


