.
#y=tanx#
To find where the graph of this function is concave or convex, we have to take the second derivative of it and set it equal to #0#; and solve for #x#. The result will be the #x#-coordinate(s) of the function's inflection point.
Then we have to try values of #x# to the right and left of this value to see if the second derivative is negative or positive. If negative that is the region where the graph is convex and if positive it is concave.
#dy/dx=sec^2x#
#(d^2y)/(dy^2)=2secxsecxtanx=2sec^2xtanx#
#2sec^2xtanx=0#
#2(1+tan^2x)tanx=0#
#tanx=sinx/cosx=0, :. x=-pi, 0, pi#
This is a rational function. As such, we have to find the value of #x# that will give us a #0# in the denominator, which will indicate the function becomes #+-oo#. At this #x# value(s) we will have vertical asymptote(s).
#cosx=0, :. x=-pi/2 and pi/2#
#1+tan^2x=0#
#tan^2x=-1# not valid
Because the function is discontinuous, we have to examine its concavity between the #x# values of the inflection points and the asymptotes. An examination of the behavior of the function to the left and right of each #x# value reveals that:
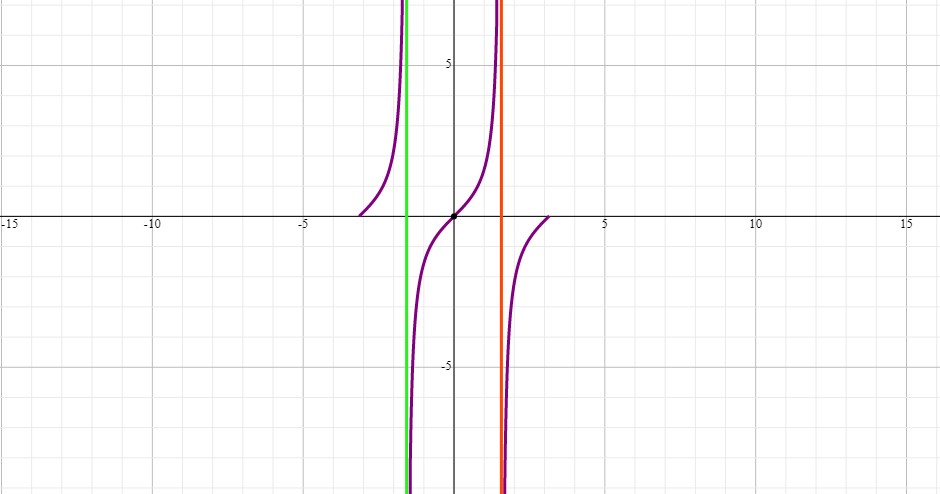
In the interval #(-pi < x < pi)#:
The graph is concave in:
#(-pi < x < -pi/2), (0 < x < pi/2)#
The graph is convex in:
#(-pi/2 < x < 0), (pi/2 < x < pi)#
The graph of #y=tanx# in the interval #(-pi < x < pi)# is: