Let's call the width of the path: #w#
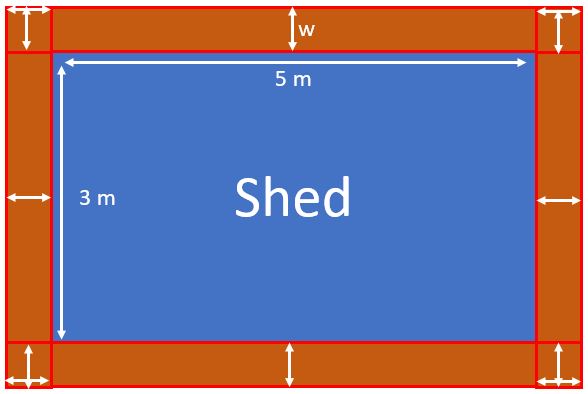
Then, we have:
- Two rectangles:#3"m" xx w#
- Two rectangles: #5"m" xx w#
- Four squares: #w xx w#
We know the total area of the path, so we can write the following equation and solve for #w#:
#2(3"m" xx w) + 2(5"m" xx w) + 4(w xx w) = 9.75m^2#
#(2 xx 3"m"w) + (2 xx 5"m"w) + 4w^2 = 9.75m^2#
#6"m"w + 10"m"w) + 4w^2 = 9.75m^2#
#(6"m" + 10"m")w + 4w^2 = 9.75m^2#
#16"m"w + 4w^2 = 9.75m^2#
#4w^2 + 16"m"w = 9.75m^2#
#4w^2 + 16"m"w - color(red)(9.75"m"^2) = 9.75m^2 - color(red)(9.75"m"^2)#
#4w^2 + 16"m"w - 9.75"m"^2 = 0#
We can now use the quadratic equation to solve this problem:
The quadratic formula states:
For #color(red)(a)x^2 + color(blue)(b)x + color(green)(c) = 0#, the values of #x# which are the solutions to the equation are given by:
#x = (-color(blue)(b) +- sqrt(color(blue)(b)^2 - (4color(red)(a)color(green)(c))))/(2 * color(red)(a))#
Substituting:
#color(red)(4)# for #color(red)(a)#
#color(blue)(16"m")# for #color(blue)(b)#
#color(green)(-9.75"m"^2)# for #color(green)(c)# ]
and solving for #w# gives:
#w = (-color(blue)(16"m") +- sqrt(color(blue)(16"m")^2 - (4 * color(red)(4) * color(green)(-9.75"m"^2))))/(2 * color(red)(4))#
#w = (-color(blue)(16"m") +- sqrt(256"m"^2 - (-156"m"^2)))/8#
#w = (-color(blue)(16"m") +- sqrt(256"m"^2 + 156"m"^2))/8#
#w = (-color(blue)(16"m"))/8 +- sqrt(412"m"^2)/8#
#w = -2"m" +- (20.29778313018444"m")/8#
#w = -2"m" +- 2.537222891273055"m"#
**For #-# the value:
#w = -2"m" - 2.537222891273055"m"#
#w = -4.537222891273055"m"#
Because we can't have a negative width we can ignore this solution.
**For #+# the value:
#w = -2"m" + 2.537222891273055"m"#
#w = 0.537222891273055"m"#
To put this solution in terms of "cm" we can calculate as"
#w = 0.537222891273055"m" xx (100"cm")/(1"m")#
#w = 0.537222891273055color(red)(cancel(color(black)("m"))) xx (100"cm")/color(red)(cancel(color(black)(1"m")))#
#w = 0.537222891273055 xx 100"cm"#
#w = 53.7222891273055"cm"#
#w = 54"cm"# rounded to the nearest centimeter.

