.
#R# is the area bounded by:
#y=2x(2-x)# and #y=0# (#x#-axis).
#2x(2-x)=0, :. x=0 and 2#
This is a parabola that opens down and crosses the #x#-axis at #x=0 and 2#
If this area is revolved about the #x#-axis the resulting solid will look like the following figure:
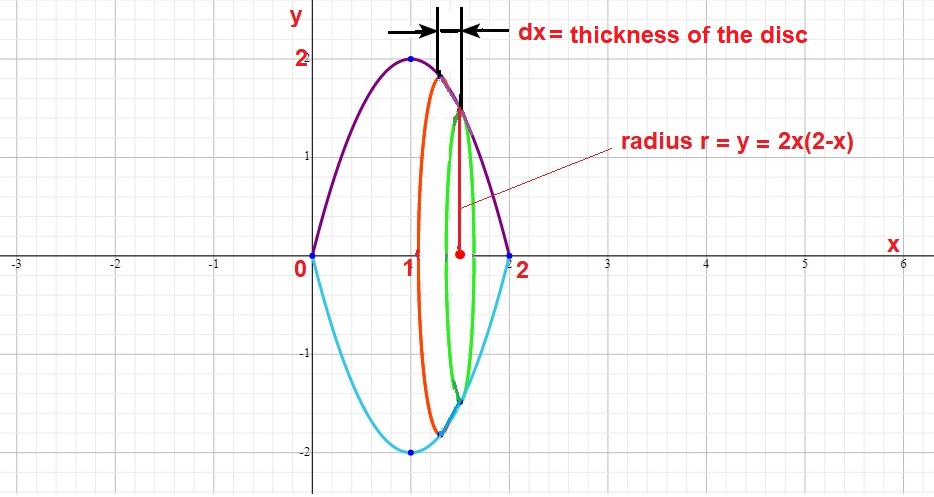
If we cut a vertical slice through the solid with a thickness #=dx# we will have a circular disc whose radius is #y=2x(2-x)#.
The area of this circular disc is:
#A=pir^2=pi[2x(2-x)]^2=pi[4x^2(x^2-4x+4)]#
#A=pi(4x^4-16x^3+16x^2)#
Then the volume of this disc would br:
#V_("disc")=pi(4x^4-16x^3+16x^2)dx#
Now, imagine that the thickness #dx# is infinitely small and there are infinite number of discs with varying radii between #x=0 and 2#.
If we take the integral of the area of this disc and evaluate it from #0 to 2# we will get the volume of the solid.
#V_("Solid")=int_0^2pi(4x^4-16x^3+16x^2)dx#
#V_("Solid")=pi(4/5x^5-4x^4+16/3x^3)_0^2=pi(4/5(32)-4(16)+16/3(8))=pi(128/5-64+128/3)=pi(384-960+640)/15=64/15pi#
If the area between the parabola and the #x#-axis is revolved around the line #y=2# the solid generated will look like the following figure:
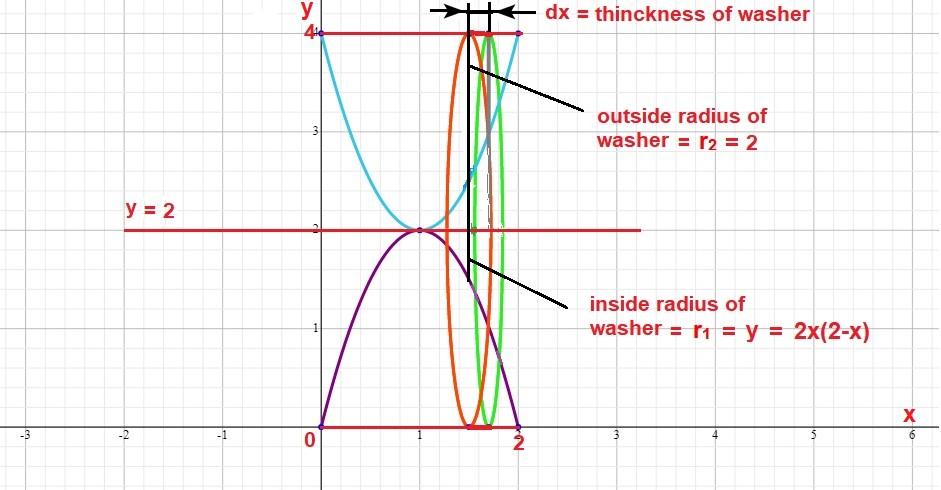
If we cut a vertical slice through this solid with a thickness of #dx# we will have a circular washer (a disc with a hole in the middle). The outer radius of this washer is #r_2=2# and the inner radius of the washer is #r_1=y=2x(2-x)#.
We can calculate the area of the washer by subtracting the area of the inner circle from the area of the outer circle:
#A_("Washer")=pir_2^2-pir_1^2=pi(r_2^2-r_1^2)=pi[4-(2x(2-x))^2]#
#A_("Washer")=pi(-4x^4+16x^3-16x^2+4)#
The volume of the washer is:
#V_("Washer")=pi(-4x^4+16x^3-16x^2+4)dx#
Now, imagine that the thickness of the washer #dx# is infinitely small and there are infinite number of washers between #x=0 and 2#. If we add the volumes of these washers together we will have the volume of the solid.
To do this, we will take the integral of the area function:
#V_("Solid")=int_0^2pi(-4x^4+16x^3-16x^2+4)dx#
#V_("Solid")=pi(-4/5x^5+4x^4-16/3x^3+4x)_0^2#
#V_("Solid")=pi(-4/5(32)+4(16)-16/3(8)+4(2))#
#V_("Solid")=pi(-128/5+64-128/3+8)#
#V_("Solid")=pi(-384+960-640+120)/15#
#V_("Solid")=56/15pi#
Therefore, the solid from revolving around the #x#-axis is greater



