Question

Under a rotation of axes, a parabola can become a hyperbola.please give a short proof or a counterexample?

Answer 1

No, in no case a parabola changes to hyperbola on rotation.

Explanation:

A standard form of conic section does not have an `xy` term. For example,

an ellipse is `x^2/a^2+y^2/b^2=1` or `(x-h)^2/a^2+(y-k)^2/b^2=1`

or parabola `y^2=4ax` or `x^2=4by` or `(y-k)^2=4a(x-h)^2` or `(x-h)^2=4b(y-k)`

or hyperbola `x^2/a^2-y^2/b^2=1` or `(x-h)^2/a^2-(y-k)^2/b^2=1`

Inn all these forms relative axes (axis pf symmetry in case of parabola) or directrix are parallel to one of axes i.e. `x`-axis or `y`-axis.

What a rotation of axes does is to rotate `x` & `y`-axis by an angle `theta` as shown in the figure below.

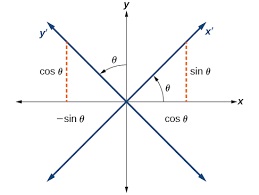
and coordinates are modified and new coordinates `(x',y')` are given by

`x'=xcostheta+ysintheta` and `y=-xsintheta+ycostheta`

Let us observe the graph of an ellipse under rotation. First graph is
graph{(x-3/(2sqrt2))^2/(5/8)+(y+1/sqrt2)^2/(5/12)=1 [-1.4, 3.4, -1.8, 0.6]}
after rotation by `theta=pi/4`, it changes it to
graph{5x^2-2xy+5y^2-9x-3y+5=0 [0.1, 1.7, 0.2, 1]}
but it remains as an ellipse.

Similarly a parabola graph{2sqrt2x^2-y=0 [-6.413, 6.387, -1.01, 5.39]} after rotation by `theta=-pi/4` appears as graph{(x-y)^2=x+y [-7.67, 12.33, -1.16, 8.84]}

However, in no case a parabola changes to hyperbola on rotation.