This integral isn't too tricky to calculate directly, but we have a shortcut. A function #f(x)# is odd if it is symmetric about the #y# axis, that is, if #f(-x) = -f(x)# for all #x in RR#.
If #f(x)# is odd, then the area above the #x# axis bounded by #f(x)# on #[0, a]# is equal in magnitude to the area below the #x# axis bounded by #f(x)# on #[-a, 0]#. Similarly, the area below the #x# axis bounded by #f(x)# on #[0, a]# is equal in magnitude to the area above the #x# axis bounded by #f(x)# on #[-a, 0]#
The sketch below illustrates the concept. Because #f(x)# is symmetric about the #y# axis, for every "positive" area to the right of the #y# axis, there is an equivalent one to the left, and vice versa.
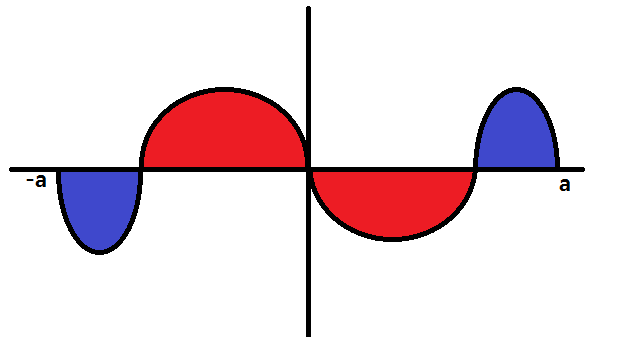
Now, seeing as we can interpret a definite integral as adding the bounded area above the #x# axis and subtracting the bounded area below, it should be no surprise that if #f(x)# is odd,
#int_(-a)^af(x)dx = 0#
And as it so happens, #x^5+6x^(1/5)# is odd, as
#(-x)^5+6(-x)^(1/5) = -x^5-6x^(1/5) = -(x^5+6x^(1/5))#
Thus, without any further calculation, we know that
#int_(-2)^2 x^5+6x^(1/5)dx = 0#


