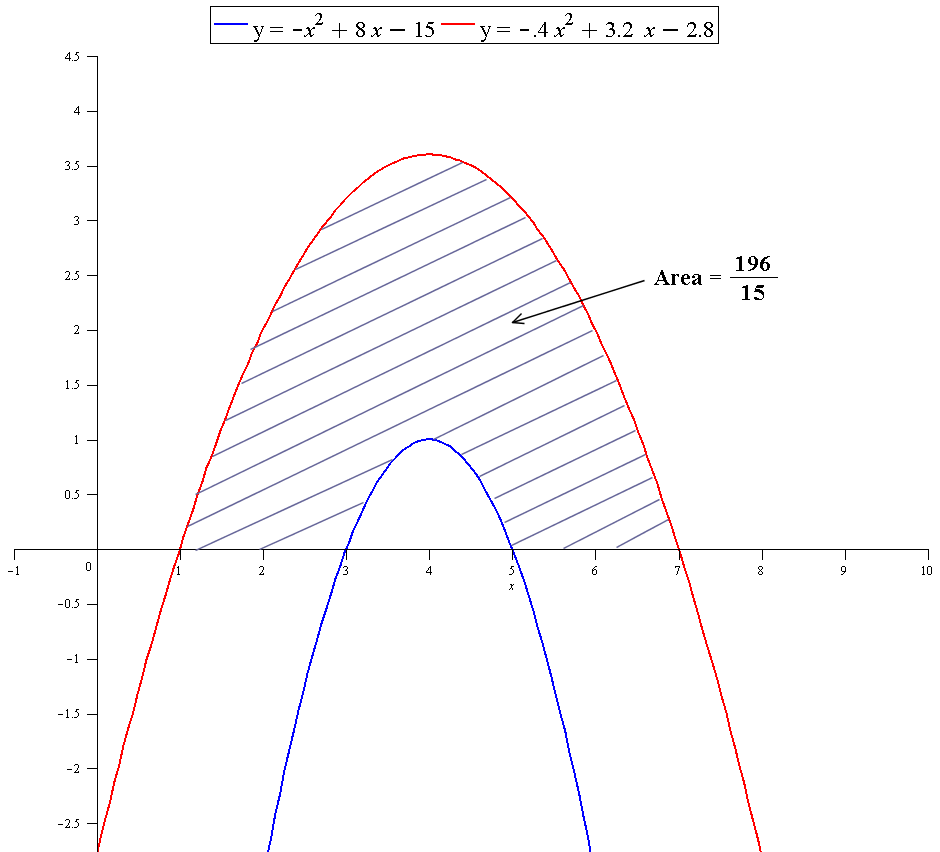
We can see from the graph, that the area we seek is the area between #g(x)# and the x axis, minus the area between #f(x)# and the x axis. We first need to find the upper and lower bounds of these functions. i.e. where they cross the x axis.
For #g(x)#, we need to solve:
For #g(x)#:
#-2/5x^2+16/5x-14/5=0#
#2x^2-16x+14=0#
Factor:
#(2x-2)(x-7)=0=>x=1 and x=7#
For #f(x)#:
#-x^2+8x-15=0#
#x^2-8x+15=0#
Factor:
#(x-5)(x-3)=0=>x=5 and x=3#
For area of #g(x)# we need the integral:
#A=int_(1)^(7)(-2/5x^2+16/5x-14/5) dx=[-2/15x^3+8/5x^2-14/5x]_(1)^(7)#
#=[-2/15x^3+8/5x^2-14/5x]^(7)-[-2/15x^3+8/5x^2-14/5x]_(1)#
Plugging in the upper and lower bounds:
#=[-2/15(7)^3+8/5(7)^2-14/5(7)]^(7)-[-2/15(1)^3+8/5(1)^2-14/5(1)]_(1)#
#=[196/15]^(7)-[-4/3]_(1)=72/5# units squared.
For area of #f(x)# we need the integral:
#A=int_(3)^(5)(-x^2+8x-15)dx=[-1/3x^3+4x^2-15x]_(3)^(5)#
#=[-1/3x^3+4x^2-15x]^(5)-[-1/3x^3+4x^2-15x]_(3)#
Plugging in the upper and lower bounds:
#=[-1/3(5)^3+4(5)^2-15(5)]^(5)-[-1/3(3)^3+4(3)^2-15(3)]_(3)#
#=[-50/3]^(5)-[-18]_(3)=4/3# units squared.
#"Area of" color(white)(88)g(x) - "Area of"color(white)(88) f(x)#
#72/5-4/3=color(blue)(196/15)# units squared.
GRAPH: