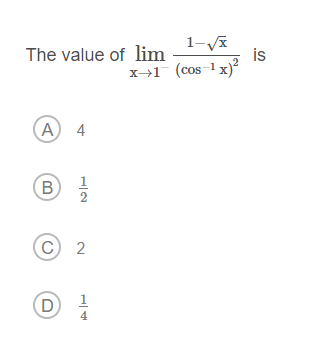Substitute #x= cost#, #t=arccosx# so that:
#lim_(x->1^-) t(x) = arccos(1) = 0#
Then:
#lim_(x->1^-) (1-sqrtx)/(arccosx)^2 = lim_(t->0^+) (1-sqrtcost)/t^2#
Rationalize the numerator:
#lim_(x->1^-) (1-sqrtx)/(arccosx)^2 = lim_(t->0^+) ((1-sqrtcost)(1+sqrtcost))/(t^2(1+sqrtcost))#
#lim_(x->1^-) (1-sqrtx)/(arccosx)^2 = lim_(t->0^+) (1-cost)/(t^2(1+sqrtcost))#
Use now the well known trigonometric limit:
#lim_(theta->0) (1-costheta)/theta^2 = 1/2#
to have:
#lim_(x->1^-) (1-sqrtx)/(arccosx)^2 = lim_(t->0^+) (1-cost)/t^2 * lim_(t->0^+) 1/(1+sqrtcost)#
#lim_(x->1^-) (1-sqrtx)/(arccosx)^2 = 1/2 * 1/2 = 1/4#
graph{ (1-sqrtx)/(arccosx)^2 [-0.51, 1.99, -0.625, 0.625]}