Question

What is the correct way to solve this? Explain step by step.

Answer 1

I got: `y=-\frac{21}{2}x+\frac{25}{2}`

Explanation:

Ok, this one is a bit steep...
First you know that the derivative `(dy)/(dx)` is the slope of the line tangent to the curve represented by your function. We can find the derivative, substitute the coordinates of your specific point getting the slope of the tangent at that point. Then we find the equation of the tangent.

Answer 2

`y = -11x +13`

Explanation:

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is `-1`).

Here we do not have an explicit equation of the form `y==(x)` as we have:

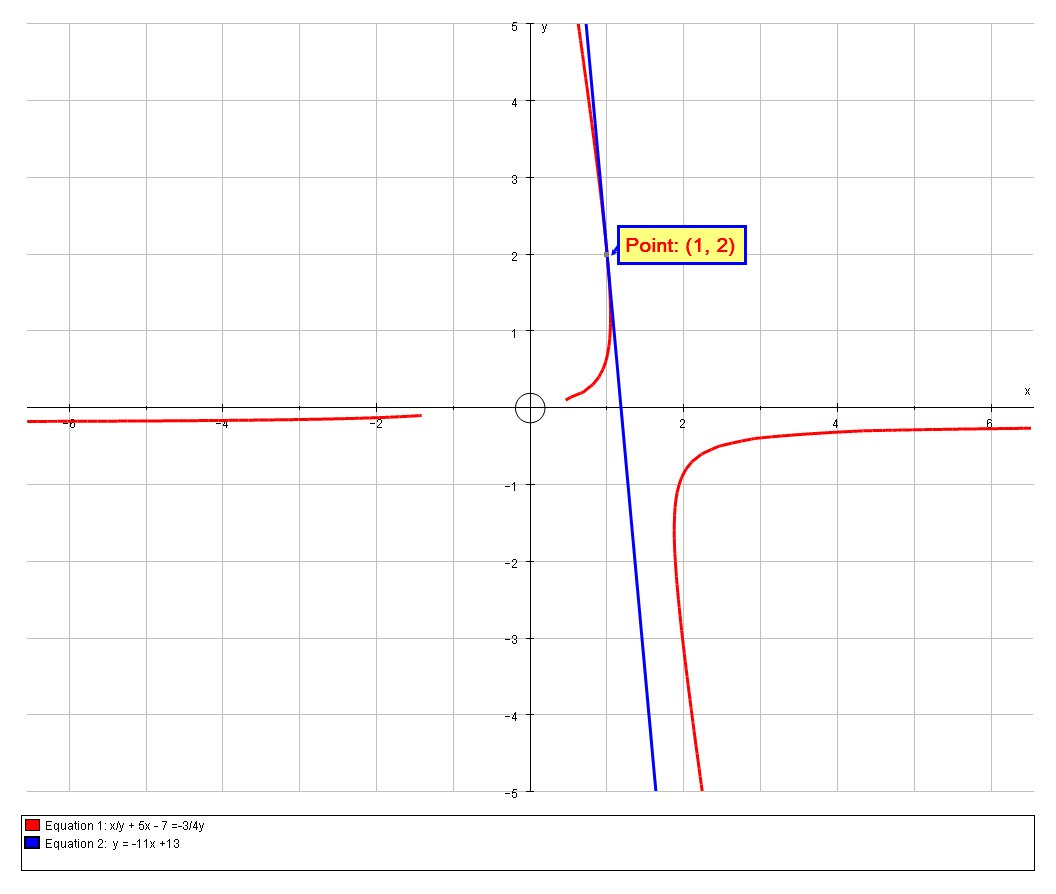
`x/y + 5x - 7 =-3/4y`

So we must differentiate implicitly, in conjunction with the quotient rule, giving:

`((y)(1) - (x)(y'))/(y^2) + 5 = -3/4y'`
`:. (y - xy')/(y^2) + 5 = -3/4y'`

Consequently we do not have an explicit expression for `y'`, but this does not matter, as all we require is `y'` when `x=1` and `y=2`:

`(2 - y')/(4) + 5 = -3/4y'`
`:. 2 - y' + 20 = -3y'`
`:.2y' = -22 => y'=-11` at `(1,2)`

So the tangent passes through `(1, 2)` and has gradient `m_T=11/2`, and using the point/slope form `y-y_1=m(x-x_1)` the equation we seek is:

`y - 2 = -11(x-1)`
`:. y - 2 = -11x+11`
`:. y = -11x +13`

We can verify this graphically: