Why area=#int_1^2 int_3^4 1/v dudv# is wrong?

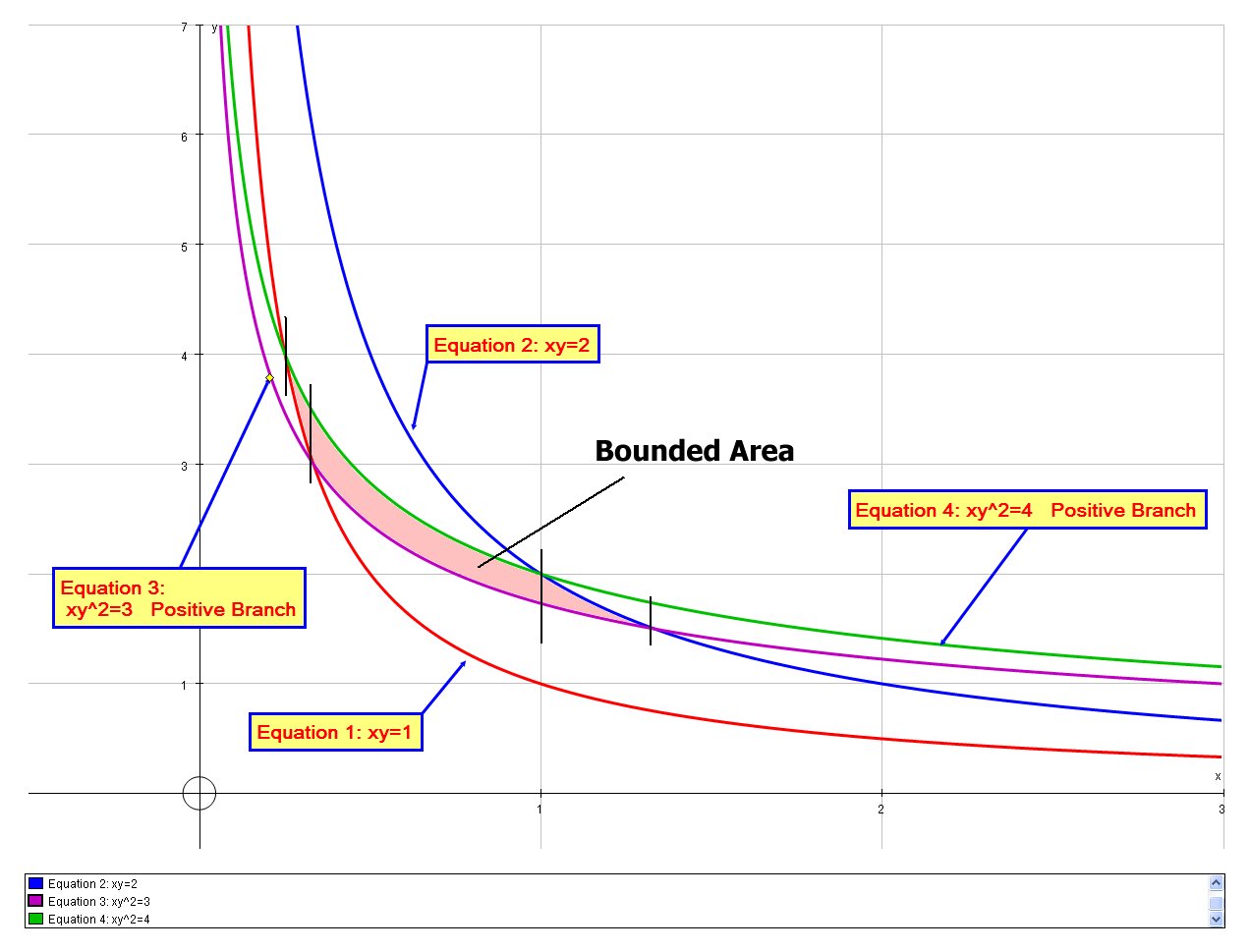
A region A is bounded by the hyperbolas #xy#=1 and #xy#= 2, and the curves #xy^2#=3 and #xy^2#= 4. The area of A is denoted by area. Use the change of variables u =#xy# and v = #xy^2#, the area of the image of the region A in the coordinate space determined by (u, v) under the transformation is called area.

And why area=#int_1^2 int_3^4 1/v dudv# is wrong?

2 Answers
Ultrilliam
Apr 12, 2018

See below

Explanation:

Your Jacobian looks good, result looks like:

#int_(u=1)^2 int_(v=3)^4 1/v dv \ du = ln(4/3)#

Transformed region:

Steve M
Apr 12, 2018

The correct double integral is:

# int_3^4 int_1^2 \ 1/v \ du \ dv # which evaluates to # ln(4/3) #

Note carefully, the order of the bounds of integration!

Explanation:

The region #bb(A)# bounded by the curves:

# xy = 1 #, #xy=2#, #xy^2=3# and #xy^2=4#

is shown graphically as follows:

Steve M

If we seek to calculate this region by conventional integration we, must split the area into multiple regions; we need to coordinates of intersection of:

# xy = 1 # and #xy^2=4 => (1/4,4)#
# xy = 1 # and #xy^2=3 => (1/3,3)#
# xy=2# and #xy^2=4 => (1, 2) #
# xy=2# and #xy^2=3 => (4/3 3/2) #

Thus we can calculate the area as

# A = int_(1/4)^(1/3) \ sqrt(4/x) - 1/x \ dx + int_(1/3)^1 \ sqrt(4/x)-sqrt(3/x) \ dx + int_(1)^(4/3) \ 2/x-sqrt(3/x) \ dx #

I will omit the calculation (as it is not really what the question is asking), and we find that:

# A = 4/sqrt(3)-2 - ln(4/3) + 6-10/sqrt(3) + 2sqrt(3)-4+ln(16/9) #
# \ \ = ln(4/3) #

The reason we would use a change of coordinates its to significantly simply the problem, as we can also denote the area problem as a double integral

# A = int int_(bb(R)) \ dxdy #

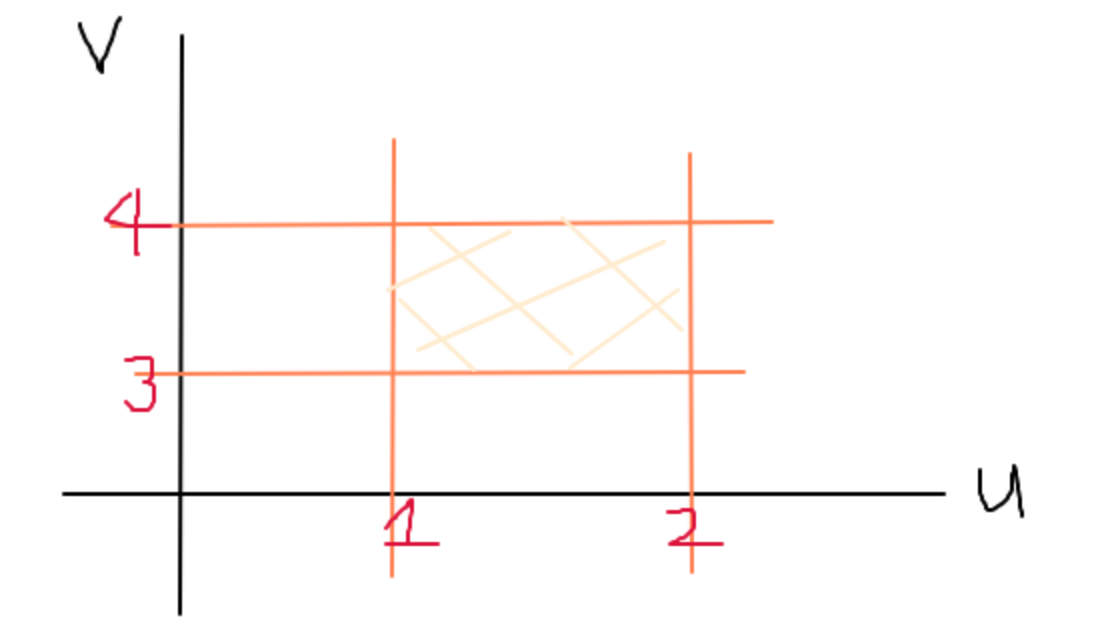
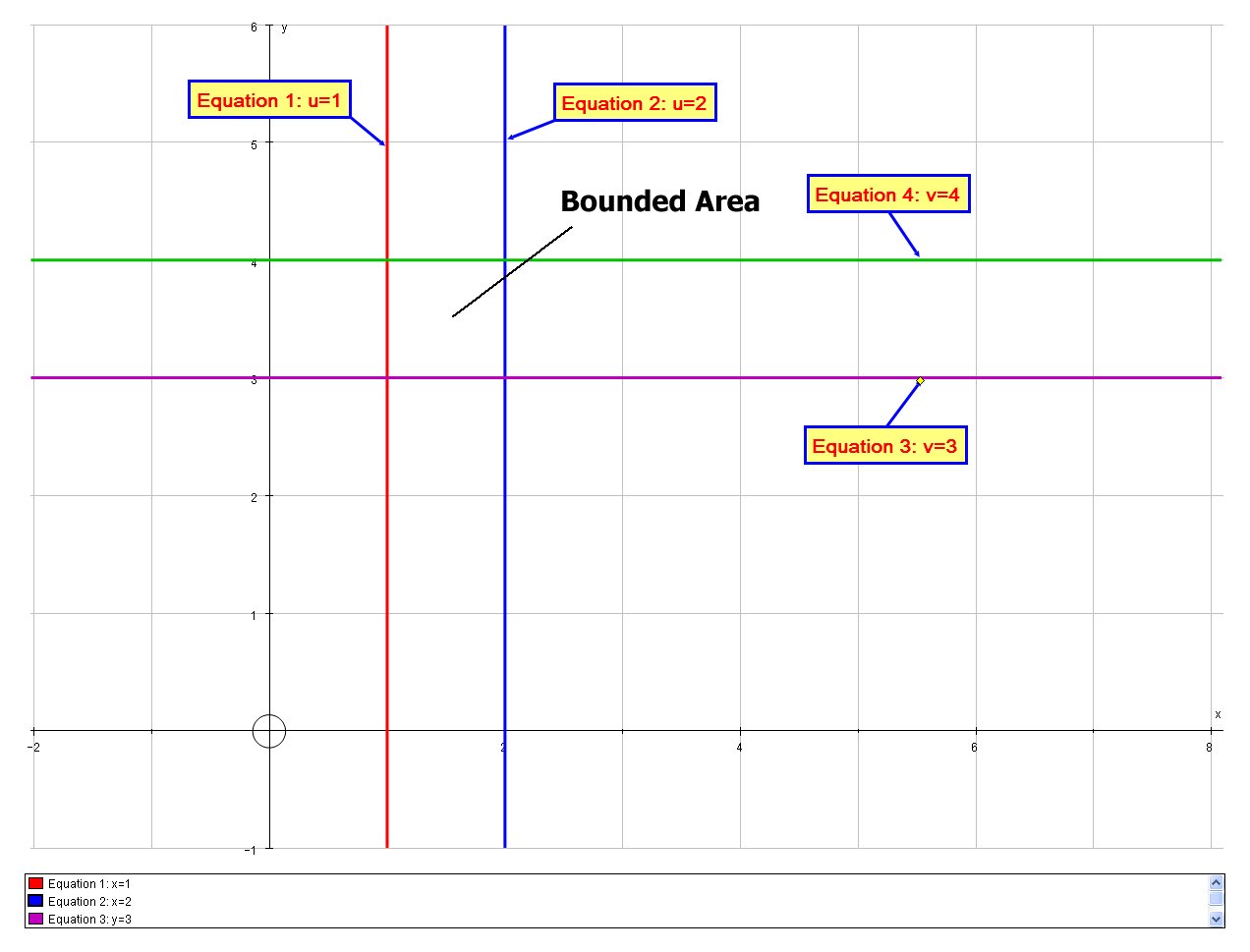
With the suggested transformation:

# u = xy # and #v=xy^2#

We can transform the problem:

# u = 1 #, #u=2#, #v=3# and #v=4#

Steve m

When we perform a transformation in a double integration we must examine the jacobian to adjust the area element #delta^2 A=delta x delta y# in the #(x,y)#-plane to #J delta u delta v# in the #(u,v)#-plane, and in this case we find that with # u = xy # and #v=xy^2# we have:

# (partial(u,v))/(partial(x,y)) = | ( (partial u)/(partial x) , (partial u)/(partial y) ), ( (partial v)/(partial x) , (partial v)/(partial y) ) | = | ( y , x ), ( y^2 , 2xy ) | #

# \ \ \ \ \ \ \ \ \ \ \ \ \ =2xy^2-xy^2 =xy^2 = v#

And we seek the Jacobian:

# J = (partial(x,y))/(partial(u,v)) = 1/v #

Hence, we can denote the area by the double integral:

# A = int int_(bb(R)) \ dx \ dy #

# \ \ = int int_(bb(R)) \ J \ du \ dv #

# \ \ = int_3^4 int_1^2 \ 1/v \ du \ dv #

# \ \ = int_3^4 1/v[u]_1^2 \ dv #

# \ \ = int_3^4 1/v \ dv #

# \ \ = [ln v]_3^4 #

# \ \ = (ln4-ln3) #

# \ \ = ln(4/3) #

Note carefully, the order of the bounds of integration!

Related questions
Impact of this question
464 views around the world
You can reuse this answer
Creative Commons License