Question

Write the equation of a circle with centre (3,-1) which is tangent to the line y=x+2?

Answer 1

`(x-3)^2+(y+1)^2=18`

Explanation:

The equation of a circle centred at the point `(3,-1)` has the equation:

`(x-3)^2+(y+1)^2 =r^2`
Where `r` is the radius of the circle.

Hence, this question asks us to find `r^2`.

We know that the line `y=x+2` is a tangent to this circle.

Note that this line has a slope of `1`

We also know that the slope of any circle centred at `(x_1,y_1)` at the point `(x,y)` is given by: `-(y-y_1)/(x-x_1)`; which in our case is:`-(y+1)/(x-3)`

Since the tangent touches the circle at a point where the circle has a slope of 1, we can replace `y=x+2` in the slope function and set this equal to 1,

`:. (-(x+2+1))/(x-3)=1`

`-x-3 = x-3`

`-2x=0 -> x=0` at the point of intersection

Now, since `y=x+2 -> y=2` at the point of intersection.

Finally, we can arrive at `r^2` by applying the point `(0,2)` to the equation of our circle.

`(x-3)^2+(y+1)^2 =r^2` at `(0,2) ->`

`(-3)^2 + (+3)^2 =r^2`

`r^2 = 9+9=18`

Hence, the equation of our circle is: `(x-3)^2+(y+1)^2=18`

This is depicted graphically below.

graph{((x-3)^2+(y+1)^2-18)(x+2-y)=0 [-18.34, 17.68, -6.8, 11.23]}

Answer 2

`(x-3)^2+(y+1)^2=18`

Explanation:

Given -
Centre of the circle `(3,-1)`
Equation of the tangent line -`y=x+2` ----------- (1)

We have to find the radius of the circle.

Find the equation of the line passing through point of tangency and the centre. It cuts the tangent at 90 degrees.

The slope of the tangent is `m_1=1`
The slope of the required line is `m_2=(-1)/(m_1)=(-1)/1=-1`

Fond the equation of the required line

`mx+c=y`
`-1(3)+c=-1`
`-3+c=-1`
`c=-1+3=2`
`c=2`

`y=-x+2` ---------------(2)

Find the point where both the lines cut each other.

`y=x+2` --------------- (1)
`y=-x+2` ---------------(2) add both

`2y=4`
`y=4/2=2`

Substitute `y=2` in equation (1)

`2=x+2`
`x=2-2=0`

The two lines cut at `(0,2)`

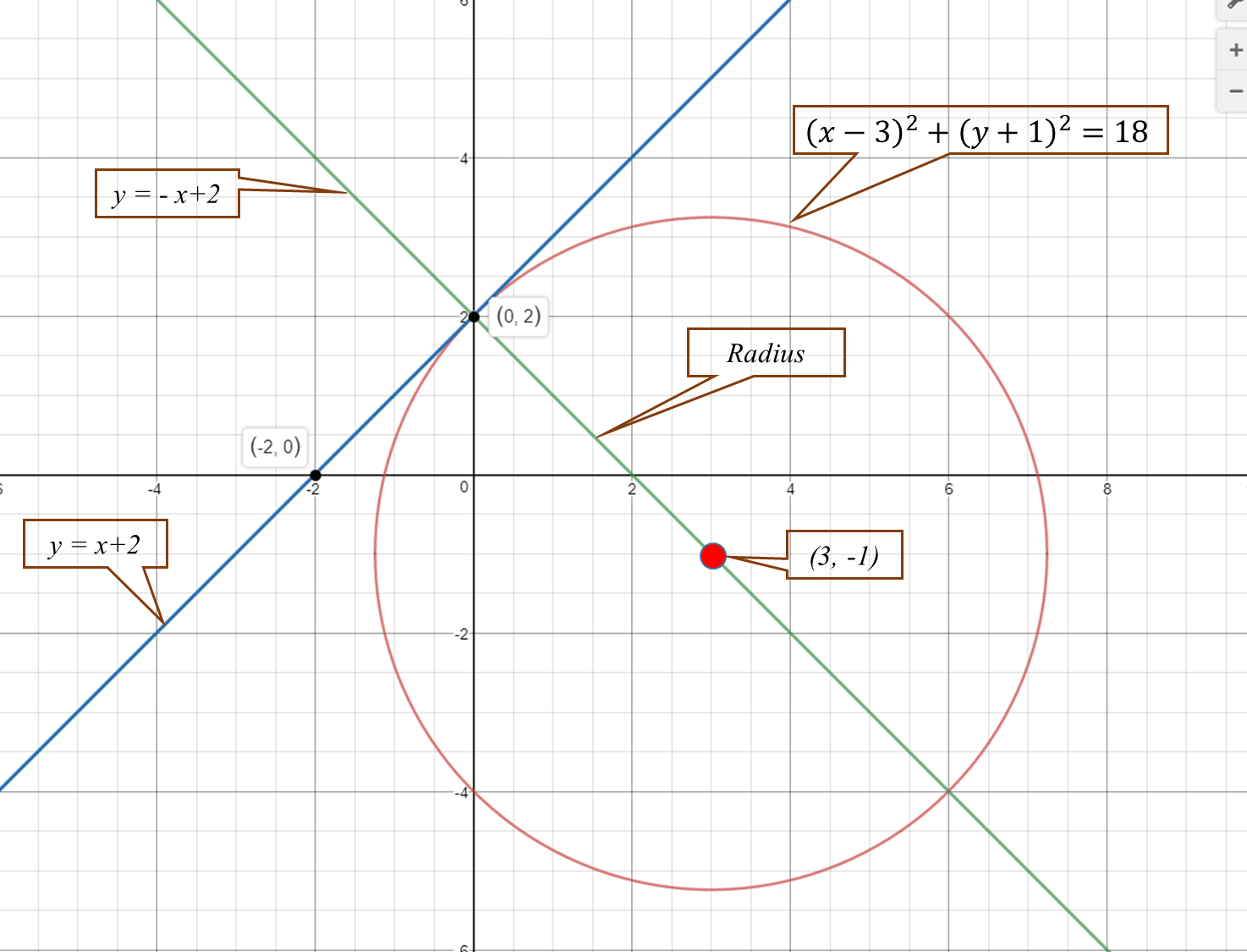
Distance between `(0,2)` and `(3,-1)` is the radius

`r^2=(x_1-x_2)^2+(y_1-y_2)^2`
`r^2=(0-3)^2+(2-(-1))^2`
`r^2=(-3)^2+(2+1)^2=9+9=18`

We have Centre and radius squared

The equation is -

`(x-h)^2+(y-k)^2=r^2`

`(x-3)^2+(y+1)^2=18`