Question

How do you solve `6cos^2x+5cosx+1=0` in the interval [0,360]?

Answer 1

`x=120^o, 240^o, 109.5^o, 250.5^o`

Explanation:

Let's take a look at the equation:

`6cos^2+5cosx+1=0`

I find it hard to focus on factoring when looking at trig functions within a polynomial, so let's just get rid of that for a second by saying:

`X=cosx` and so therefore:

`6X^2+5X+1=0`

Now let's factor:

`(3X+1)(2X+1)=0`

And so therefore:

`3X+1=0 => X=-1/3`

`2X+1=0 => X=-1/2`

And so:

`X=cosx=-1/3, -1/2`

Ok - so now what?

Cosine is negative where the adjacent is negative (that is to say, where the line along the x-axis making the triangle we're looking at runs along the negative part of the axis). So we're in quadrants 2 and 3.

Let's work out the reference angles, starting with `cosx=-1/2`:

This one is a special triangle - the 30/60/90 triangle - and so we know the reference angle is `60^o` or `pi/3`. We can take `pi/3` away from `pi` to see the angle in Q2 (`pi-pi/3=(2pi)/3`) and add to `pi` to see the angle in Q3 (`pi+pi/3=(4pi)/3`):

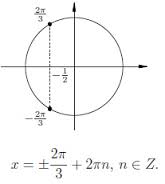
And now `cosx=-1/3`:

This one isn't so neat. It's roughly `70.5^o`, which will give us `180-70.5=109.5^o` and `180+70.5=250.5^o`. (I'm hoping my fellow answer writers will fill in a clean radian fraction but due to time constraints I need to leave this part of the answer undone).