Question

How do you graph the inequality `6x+3y>12`?

Answer 1

Let's isolate `y`:

`6x+3y > 12`

`3y > 12 - 6x`

`y > (12-6x)/3`

`y > 12/3 - (6x)/3`

`y > 4 - 2x`

Now we have the information we need to graph this:

This looks an awful lot like slope-intercept form, where `y = color(orange)(m)x + color(green)(b)` with `color(orange)(m)` being the slope and `color(green)(b)` being the `y`-intercept

In our case, we have `y > color(orange)(-2)x + color(green)(4)`

This tells us that our graph has a slope of `-2/1` or down `1`, over `1` and a `y`-intercept at `4`.

graph{y = -2x+4}

Now, we need to figure out if the graph shows a dashed or solid line. This is pretty simple: does the inequality sign include a value `(>= or <=)` or does it exclude values (`< or >`)#? If it includes values, it is a solid line. If it does not, and excludes values, then we use a dashed line.

So in our case, our graph will have a dashed line because it has the `>` sign.

The question is, which side of the graph do we include? There are a few ways to check, but I like a simple method: pick two points, one from each side of the graph. THESE POINTS CANNOT BE ON THE GRAPH Whichever one makes the statement true is correct

Let's pick `(0, 0)` and `(2, 2)` No need to make the math hard :)

`* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *`

`0 > -2(0) + 4`

`0 > 4`

is this true? is `0` larger than `4`? No it is not, so the inequality isn't on this side

`* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *`

`2 > -2(2) + 4`

`2 > -4+4`

`2 > 0`

is this true? is `2` larger than `0`? Yes it is, so the inequality is on this side

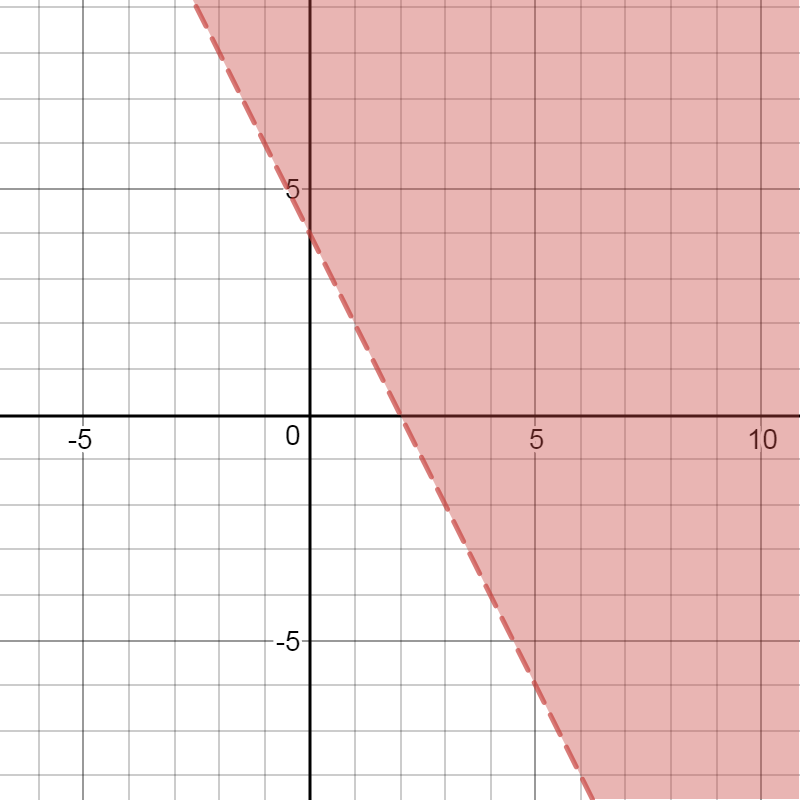
*This graph was obtained form https://www.desmos.com/calculator/sqb3smcrdv*