Slope
Key Questions
-
The slope is a number that tells you how much y changes when x changes.
For example: a slope of 5 means that for each change in x of 1 unit (for example between 6 and 7) the correspondig y changes of 5 units.
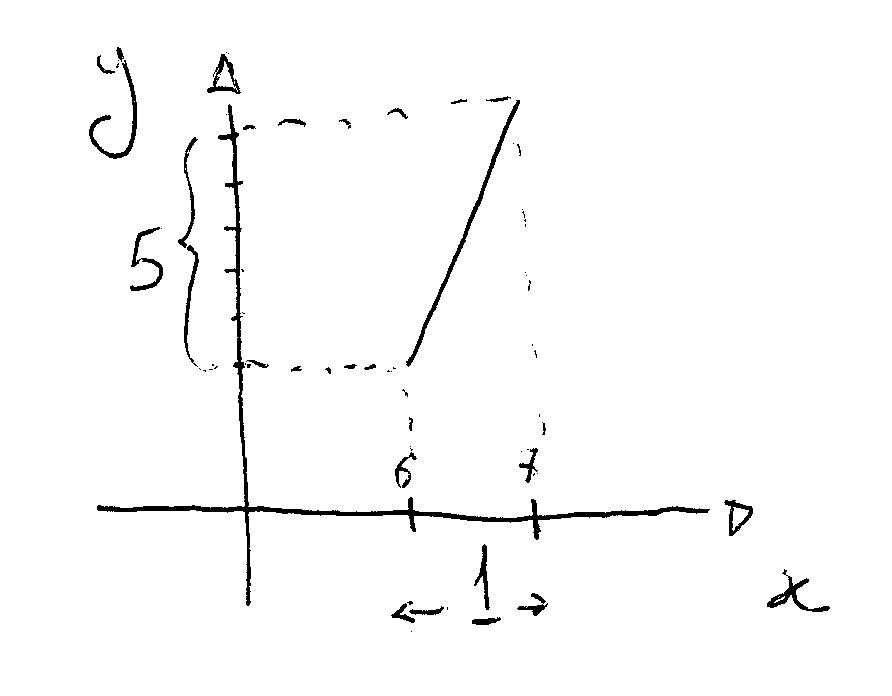
This is for a positive slope, so that your value of y is getting...bigger!!!The negative slope is the opposite, it tells you of how much y decreases for each increas of 1 unit in x.
A slope of -5 tells you that the value of y decreases of 5 units in the 1 unit interval of x:
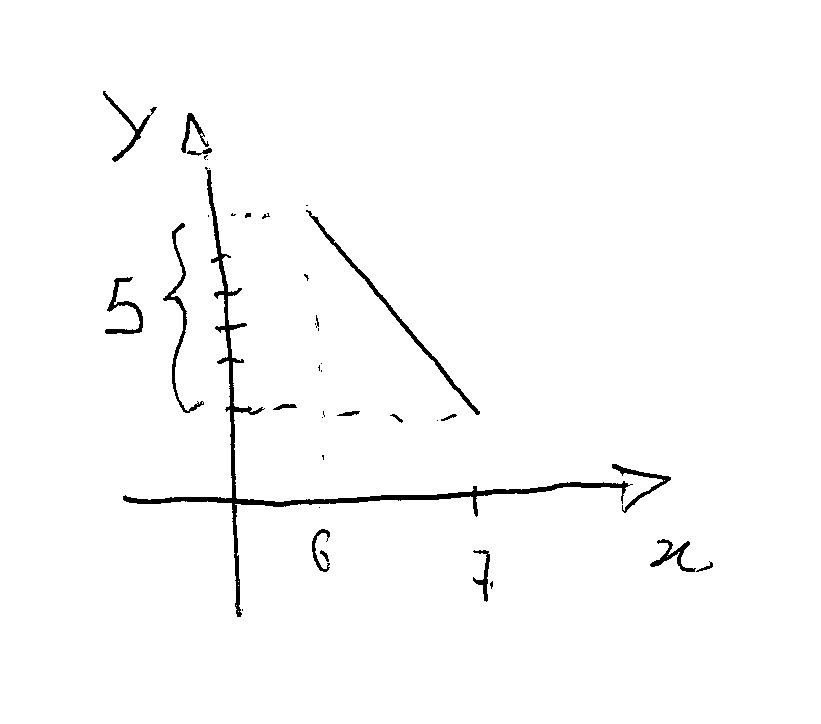
As you may guess the slope is a measure of the "inclination" of your line!!!
Try to guess what a slope of zero means!!!!!!
-
Answer:
See below:
Explanation:
The steepness of a line is essentially the slope. When we see a line oriented from bottom left to upper right, it has a positive slope. A negative slope would be depicted by a line going from the upper left to bottom right.
Slope values increase the higher the number is: For instance, a line with a slope of
#2# is steeper than a line with a slope of#1/2# .Hope this helps!
-
Use the slope formula (
#m = (y_2 - y_1)/(x_2 - x_1)# ) to calculate the slope given two points#(x_1, y_1)# and#(x_2, y_2)# .Here is an example of finding the slope, given two points (-2,3) and (4,-5).
#(-2, 3) = (x_1, y_1)#
#(4, -5) = (x_2, y_2)# #m = (y_2 - y_1)/(x_2 - x_1)# #m = (-5 - 3)/(4 - (-2))# #m = (-5 - 3)/(4 + 2)# #m = (-8)/(6)# #m =-4/3# The slope of of (-2,3) and (-4,5) is
#-4/3# -
Nuzhat has already discussed how you can find the slope of a line from two points that lie on the line. I'll discuss two other methods of finding the slope from a graph.
1. From the angle made with the x-axis
Since the slope of a line is basically the ratio of the y-component of the line to its x-component,
The slope of a line can be found out by taking tangent of the angle between the given line and the x-axis.
Consider the following figure:
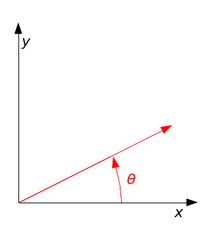
In this case, the angle between the x-axis and the line is
#theta# .Therefore,
Slope of the given line =#tantheta# Note: Angles in the counterclockwise direction are taken as positive, and those in the clockwise direction are taken as negative.
For example, if the angle between the x-axis and the given line is
#30^o# ,Slope of the given line =
#tan30=1/sqrt3# 2. From the equation of the line
The slope of a line can also be determined from its equation. The standard form of the equation of a line is:
#Ax^2+By+C=0# where
#A,B and C# are some constants.First, the equation of the line must be written in the standard form.
Then, the slope of the line =
#-A/B# For example, let the equation of the given line be
#x^2+3=2y# .Rewriting in the standard form, we get:
#x^2-2y+3=0#
and we can see that:
#A=1#
#B=-2#
#C=3# Therefore, the slope of the line
#=-A/B=-(1)/(-2)=1/2# -
Answer:
Slope is the change in the y values divided by the change in the x values
Explanation:
#"slope"="rate of change in y"/"rate of change in x" ="rise"/"run"# #(color(blue)(x_1),color(blue)(y_1))# #(color(red)(x_2),color(red)(y_2))# #color(green)m =(color(red)(y_2)-color(blue)(y_1))/(color(red)(x_2)-color(blue)(x_1))# Is is often expressed as rise over run.
Questions
Graphs of Linear Equations and Functions
-
Graphs in the Coordinate Plane
-
Graphs of Linear Equations
-
Horizontal and Vertical Line Graphs
-
Applications of Linear Graphs
-
Intercepts by Substitution
-
Intercepts and the Cover-Up Method
-
Slope
-
Rates of Change
-
Slope-Intercept Form
-
Graphs Using Slope-Intercept Form
-
Direct Variation
-
Applications Using Direct Variation
-
Function Notation and Linear Functions
-
Graphs of Linear Functions
-
Problem Solving with Linear Graphs